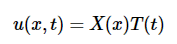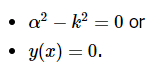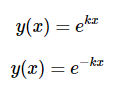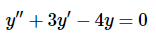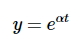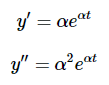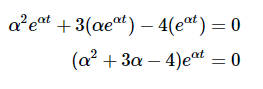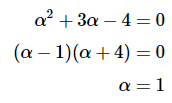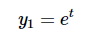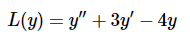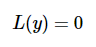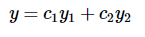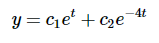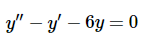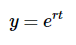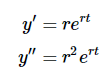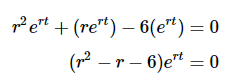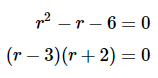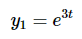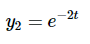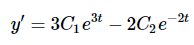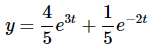|
2.2: 分离变量的方法学习目标介绍变量分离技术作为求解波动方程的方法
求解波动方程需要确定函数u(x,t)求解表示波在任意位置x处振幅的偏微分方程在任意时间t
该波动方程是一种涉及两个变量的二阶偏微分方程(PDE)-xt和偏微分方程(PDE)与仅涉及单变量函数的常微分方程(ODE)不同。然而,这种差异使得偏微分方程的求解难度显著增加。事实上,绝大多数偏微分方程无法通过解析方法求解,而那些可以解析求解的特殊偏微分方程类通常需要将偏微分方程转化为一个或多个常微分方程,然后分别求解。其中一种方法是分离变量法。
变量分离方法波动方程的变量分离方法的一般应用包括三个步骤:
l 我们找到波动方程的所有解,其一般形式为
对于某个函数X(x)这取决于x但不是t以及一些函数T(t)这仅取决于t,但不是x。当然,期望方程2.2.1的所有解都满足这个要求是不现实的。然而,如果找到一组解{Xi(x)Ti(t)},则为这种形式由于波动方程是一个线性方程,
也是任意常数ci的选择的解。
根据系统知识对解施加约束。这些称为边界条件,规定了u(x,t)的值在极限点(“边界”)处。这与初值问题中的解类似,条件为x(ti)在特定时间ti指定。然后,目标是选择常数ci见公式2.2.2使边界条件也得到满足。
变量分离法是求解偏微分方程最广泛使用的技术之一,它基于方程的解是可分离的假设,即最终解可以表示为多个函数的乘积,每个函数仅依赖于一个自变量。如果这个假设是不正确的,那么从分析中可以明显地看到明显违反数学原理的行为。
固定在两点之间的振动弹簧如第2.1节所述,字符串示例u(x,t)的解对于所有xt和假定为两个函数的乘积:X(x)以及T(t),其中X(x)仅是x的函数,不以及T(t)是t的函数,但不是x.
替换方程式2.2.3代入一维波动方程(方程2.2.1)得到
因为X不是t的函数T和不是x的函数,公式2.2.4可以简化
合并依赖于x的表达式见公式2.2.5的左侧以及t右侧的结果是
公式2.2.6是一个有趣的方程,因为每一侧都可以设置为一个固定的常数K作为对所有t值以及x的唯一有效解。因此,该方程可以分为两个常微分方程:
因此,通过替换新方程解的形式(方程式2.2.3)进入原始波方程(方程2.2.1),我们转换了两个变量的偏微分方程(x和t)化为两个常微分方程(包含一个或多个自变量及其导数的微分方程)。每个微分方程仅涉及一个自变量(x或t).
l 如果K=0,那么解决方案就是微不足道的u(x,y,)=0的解(即不存在波) l 如果K>0,即方程2.2.8的通解是
在该阶段,公式2.2.9这意味着两个常微分波动方程的解将是一个无限数量的波,没有量化来限制允许的波(即,任何A值以及B是可能的)。当考虑到边界条件时,将一般解缩小到特定解。
该问题的边界条件是波幅在弦的两端等于零
对于所有时间t。
应用方程2.2.10中的两个边界条件以及2.2.11代入方程2.2.9中的通用解得到AB之间的关系:
和
忽略琐碎的解决方案解决此问题的一个方法是A=B=0,但这是从K=0得出的简单解,我们忽略它,因为它除了知道0=0之外,没有提供任何物理上的解决方案,这不是一个鼓舞人心的结果。
两个方程 2.2.7 和 2.2.8 可以概括为以下方程
这里 k是一个实常数(即不是复数)。方程 2.2.14是齐次二阶线性微分方程。这些类型的微分方程的一般解形式为
其中α是系统约束条件下的常数。代入公式2.2.15代入公式2.2.14结果
要满足此方程,要么
后者是简单的解决方案,被忽略,因此
所以
因此,一般方程2.2.14有两个解。,如预期的二阶微分方程(一阶微分方程只有一个解),这是通过代入α得到的结果数值来自公式2.2.18代入公式2.2.15
一般解可以是这两个方程的任意线性组合
例 2.2.1 :常规解决方案求解
解答 策略是寻找形式为的解
原因在于很久以前一些天才发现了这个原理,它确实有效。现在计算导数
代入微分方程可得到
现在除以eαt得到
和 α=−4
我们可以得出结论,两个解是
和
现在让我们
很容易验证,如果 y1和 y2是解,那么
然后
也是一种解。更具体地说,我们可以得出结论:
表示一个二维解族(向量空间)。稍后我们将证明这是解空间的最一般描述。
例 2.2.2 :边界条件求解
其中已知y(0)=1和 y′(0)=2
解答 和以前一样,我们寻求以下形式的解
现在计算导数
代入微分方程可得到
现在除以 ert得到
我们可以得出结论,两种解是
和
我们可以得出结论
表示解的二维族(“向量空间”)。现在使用初始条件来查找 1=c1+c2 我们有那个
将初始条件代入 y′得到 2=3c1−2c2
这是一个由两个方程和两个未知数组成的系统。我们可以使用线性代数来得出 c1=4/5 和 C2=1/5
最终的解是
当K>0时,方程2.2.7的通解和2.2.8分别在时间和空间上呈振荡状态,如下一节所讨论。 上一篇2.3:微分方程的震荡解下一篇2.1:一维波动方程 |