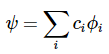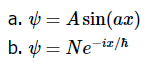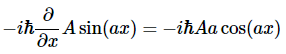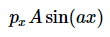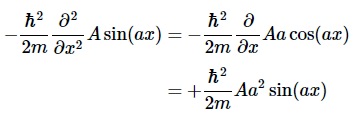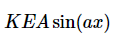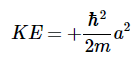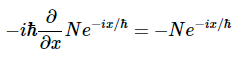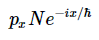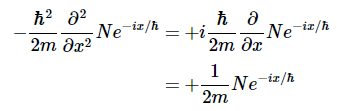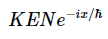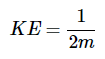|
3.3: 薛定谔方程是一个特征值问题学习目标l 认识到每个量子力学可观测量都是通过不同算子的特征值问题来确定的。 l 确认特定波函数是否为某一特定操作的本征函数,并提取对应的可观测量(即本征值)。 l 认识到薛定谔方程,就像所有可测量的物理量一样,也是一个特征值问题,其特征值被赋予总能量。 l 识别并操作多个常见的量子力学算子
根据定义,作用于函数的运算符会生成另一个函数,但当生成的函数与原始函数成比例时,会出现特殊情况。
通过引入比例常数k,该案例可以用等式来表示。
并非所有函数都能像方程3.3.2那样解方程。如果函数确实存在,那么ψ被称为特征函数,其中k为常数被称为特征值(这些术语是德语的混合体,纯英语的对应词分别是“特征函数”和“特征值”)。求解特征值问题在大多数线性代数课程中都有讨论。
在量子力学中,每个实验可测量值a是特定算子(A^)的特征值。
a特征值表示A^算符的可能测量值。经典地,a可以被允许连续变化,但在量子力学中,a通常只允许使用部分值(因此具有量子特性)。时间依赖和时间独立的薛定谔方程是量子力学中最著名的本征值方程实例,其本征值对应于量子系统的允许能级。
作用于ψ(x)的左侧对象是运算符的一个示例。
实际上,它要求我们对ψ(x)求二阶导数,将结果乘以−(ℏ2/2m)然后加上V(x)ψ(x)量子力学涉及多种类型的算子。然而,其中一个特别重要,因为它出现在薛定谔方程的左侧。这个算子被称为哈密顿算子,并用符号表示为
因此,含时态薛定谔方程可以(更常见地)写成
和与时间无关的薛定谔方程
注意方程3.3.8的函数形式与方程3.3.2中的通用特征值方程相同。其中,特征值即为允许的总能量E。 哈密顿量是以爱尔兰数学家哈密顿的名字命名的,它来源于来源于基于总能量的经典力学公式,H=T+V,而不是牛顿第二定律,F=ma。方程式3.3.8表示哈密顿算子作用于波函数,从而产生能量E,这是一个标量(例如,用焦耳表示)乘以波函数。
对应原则注意H^源自经典能量公式p²/2m+V(x),只需替换p→−iℏ(d/dx),这是尼尔斯·玻尔最初提出的对应原理的一个例子,该原理指出,量子理论描述的系统的行为在量子数很大的极限下重现经典物理。
量子力学的一个基本原则是,每个物理可观测量都有一个对应的算符。物理可观测量是指任何可以被测量的量。如果描述系统的波函数是某个算符的本征函数,那么通过该算符作用于本征函数,可以得到该可观测量的值。此时,该可观测量的值即为本征值,系统也就处于一个本征态。方程3.3.8该原理以数学方式表述了能量作为可观测量的情况。如果波函数不是操作的本征函数,那么测量将给出一个本征值(根据定义),但每次测量得到的本征值不一定相同(这一点将在后续章节中详细讨论)。
常用运算符虽然理论上我们可以提出无限数量的运算符,但在实践中有一些比其他运算符更重要。
Linear Momentum(线性动量):一维运动粒子的线性动量算符(x方向)是
并且可以在三个维度上推广:
位置一维运动粒子的位置算符(x方向)是
并且可以在三个维度上推广:
这里r⃗=(x,y,z) 动能传统上,粒子在一维中移动的动能(x方向)的
从量子力学上讲,对应的动能算符是
并且可以在三个维度上推广:
角动量角动量需要更复杂的讨论,但它是位置算子r^和动量算符p^的叉积。
哈密顿量哈密顿算子对应于系统的总能量
在三维中的哈密顿量是
总能量含时薛定谔方程的能量算子
方程3.3.6的右侧哈密顿算子不仅决定了系统的能量,还规定了波函数随时间的演化过程。
这方面将在其他地方更详细地讨论。
特征状态、特征值、波函数、可测量对象和可观察对象一般来说,波函数给出了所讨论系统的 “系统状态”。它存储了观察者可用的有关系统的所有信息。在量子力学的讨论中,术语本征态和波函数经常互换使用。术语 eigenvalue 用于表示与波函数相关的可测量量的值。 l 若要测量粒子的能量,必须使用哈密顿算子对波函数进行操作(方程3.3.6)。 l 若要测量粒子的动量,必须使用动量算子对波函数进行操作(方程3.3.9。 l 若要测量粒子的位置,必须对波函数应用位置算符(方程3.3.11。 l 若要测量粒子的动能,必须使用动能算符对波函数进行操作(方程3.3.14)。
在讨论哈密顿量H^的本征态时,其中的特征值代表能量;而在动量算符的框架下,这些特征值则对应粒子的动量。然而,并非所有波函数(ψ)是算符(ϕ)的本征态。如果它们不是,它们通常可以写成本征态的叠加。
将在后续章节中对此进行更详细的讨论。
虽然波函数可能不是某个可观测量的本征态,但当该可观测量作用于波函数时,波函数会变成该可观测量的本征态,此时只能观察到本征值。换句话说,波函数‘坍缩’成可观测量的本征态。由于量子力学中的算符形式各异,它们对应的本征态通常也不同。例如,如果波函数是总能量的本征态,那么它就不可能是动量的本征态。
如果一个波函数是某个算子(例如动量)的本征态,那么这个状态不一定是另一个算子(例如能量)的本征态,尽管并非总是如此。
测量后,波函数立即成为与该测量相关的算符的本征态。测量后波函数的变化情况是另一个话题。
例 3.3.1确认以下波函数是线性动量和动能的特征态(或两者都不是或两者都是):
策略他的问题是询问特征值方程是否适用于这些算子和波函数。这实际上是在问这些波函数是否满足方程3.3.2的条件。使用方程3.3.9和3.3.14中的运算符,即这些方程是否成立:
其中px以及K E是这些算子的可测量值(特征值)。
解决方案 a我们来评估线性动量特征值问题(方程3.3.21)的左侧。
并与方程3.3.21的右侧进行比较
这些是不同的,所以这个波函数不是动量的本征态。 我们来看动能本征值问题的左侧(方程3.3.22)
并与右侧进行比较
这些是相同的,因此这个特定的波函数是动能的本征态。此外,测量得到的动能将是
解决方案 b我们来看方程3.3.21的左边用于线性动量
和方程的右侧 3.3.21
它们是相同的,因此该波函数是具有动量的动量的特征态 px=−N 我们来看方程3.3.22的左边动能
以及右侧
因为这些是相同的,所以这个波函数是动能的本征态。测得的动能将是
该波函数是动量和动能的特征态。 |