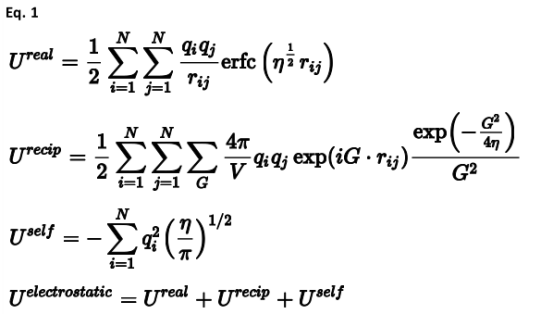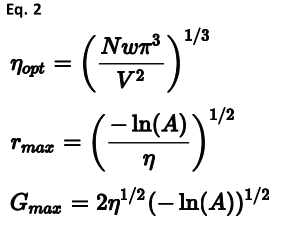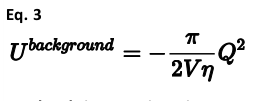4.3长程势-4.3.2三维周期体系中的库仑相互作用

当考虑离子材料时，库仑相互作用是迄今为止的主导项，通常可以代表高达总能量的90%。尽管库仑定律给出了最简单的形式，但它是对周期体系进行评估最复杂的。这是因为库仑能量是由一个条件收敛的级数给出的，所以除非指定某些附加条件，否则它对于无限三维材料是不明确的。这是因为离子之间的相互作用随着r的逆幂衰减，但相互作用离子的数量随着球体的表面积增加而增加，由4πr²给出。因此，相互作用的能量密度随着距离的增加而增加，而不是衰减。对于小到中等尺寸的3D周期体系，通过Ewald方法最有效地实现求和（Ewald，1921；Tosi，1964）。在这里，施加电荷中性和零偶极矩的条件，以产生具有明确定义的极限的收敛级数。为了加速评估，对库仑项进行拉普拉斯变换，然后将其分离为两个分量，一个分量在实空间中快速收敛，另一个分量则在倒数空间中快速衰减。从概念上讲，这种方法可以被视为对以每个离子为中心的高斯电荷分布进行加减。得到的实空间和倒数空间的表达式，以及离子的自能，如下所示：

其中：

q是离子上的电荷

G是倒易晶格矢量（排除特殊情况G=0）

V是晶胞的体积

η是控制实空间和倒易空间之间功分的参数

还应该注意的是，尽管倒数空间项被写为原子对上的两体相互作用，但为了更有效的评估，它可以被重写为离子上的单个和。上面详细介绍的方法仍然为实数和倒数空间的截止半径的选择留下了余地。以一致的方式定义这些项的一种方法是，在给定的指定精度a下，最小化两个系列中要评估的项的总数。这导致了以下表达式：

上述公式的推导是由Jackson和Catlow（1988）给出的，只是w的值被隐含地假设为1.通常发现，由于实现因素的影响，反映倒数空间和实数空间中计算电荷比率的参数w不是体系大小的函数。此参数的调整可以为大型体系带来显著的好处。

对于基本的Ewald求和，已经提出了一些修改，以加速其对大型体系的评估，最著名的是粒子网格和快速多极方法。此外，对于大的晶胞，有一些竞争性的方法纯粹在真实空间中操作，并且随着尺寸的增加而线性扩展，例如分层快速多极方法，尽管必须注意通过施加零偶极要求来获得相同的限制结果。后一种方法也可以用于加速有限团簇的库仑能量的计算。

原则上，也可以计算具有净偶极子的体系的库仑能量。对埃瓦尔德能量的校正的性质可以被确定为晶体形状的函数。

然而，使用这种校正的复杂性在于，它取决于晶体的宏观偶极和由于粒子周围环境而产生的任何补偿电场。因此，偶极矩通常定义不清，因为它取决于表面以及本征材料。即使忽略了表面效应，偶极矩的定义也是模糊的，因为在晶格矢量平移原子图像的情况下，算子不是不变的。因此，埃瓦尔德的结果被认为是决定性的。

类似地，只要在构建热力学循环时注意，就可以弛豫电荷中性约束，并对带电的超级单元进行计算（Leslie和Gillan，1985）。这通常用于探测缺陷能量学，作为Mott-Littleton方法的替代方法。这里，净电荷Q（Q=∑qi）被均匀的背景电荷中和，导致能量校正：