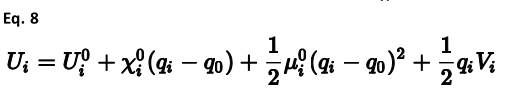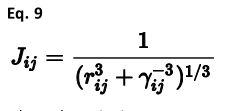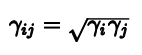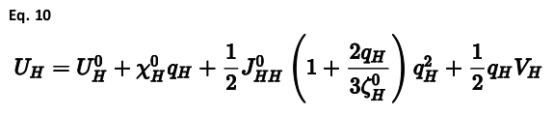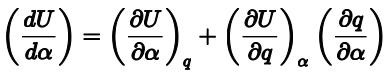4.3长程势-4.4.5原子电荷的测定

在大多数模拟中，为了简单起见，离子上的电荷是固定的（也就是说，它们与几何结构无关），并且它们的大小是与其他力场参数一起参数化确定的，或者是从量子力学信息中提取的。在后一种情况下，会出现什么是合适的电荷的问题，因为这取决于密度矩阵是如何划分的。尽管穆利肯分析通常被用作标准，但这不一定是力场中使用的最佳电荷定义。可以说，一个更好的选择是使用Born有效电荷（见Baroni等人，2001），该电荷描述了离子对电场的响应。如果电荷纯粹被视为参数，那么形式电荷的使用是方便的，因为它消除了自由度，并最大限度地提高了力场的可转移性，尤其是对带电缺陷的可转移。

使用固定电荷的替代方案是允许将电荷确定为几何形状的函数。有充分的证据表明，在某些情况下，电荷对环境的依赖性非常重要。例如，冰中的水的结合能比水二聚体中的结合能大得多。这是由于固态中O-H键极性增加的结果，不能用简单的两体模型正确描述。为了实现可变电荷方案，需要一个对力场模拟实用的简单哈密顿量。因此，关于几何相关电荷的大多数理论方法都是基于电负性均衡的概念。

这里，原子的能量相对于电荷q展开，其中能量相对于电荷的一阶导数是电负性χ，二阶导数是硬度μ：

上述表达式中的最后一项是由于体系中的其他原子与库仑势的相互作用。在这个方程中，项q0是假设电负性参数为二次方的电荷。通常此值为0。

通过同时求解所有原子的耦合方程组，这会导致一组电荷平衡体系的化学势。这种方法在一般情况下有两种变体。在第一种方法中，以van Genechten等人（1987）的工作为代表，库仑相互作用J用简单的1/r形式描述。Rappe和Goddard（1991）在他们的QEq方法中使用的另一种方法是使用阻尼库仑势，该势允许在短距离内，相互作用由电子密度的重叠引起，而不仅仅是由简单的点离子引起。因此，在QEq中，势能是基于s轨道与适当指数的相互作用来计算的。另一种变体试图以数学上更有效的形式封装库仑相互作用的短程阻尼（Njo等人，1998）：

其中成对项γij通常根据组合规则来确定，以便最小化自由参数的数量：

在氢的情况下，电荷在氢化物和质子极限之间的变化是如此极端，以至于有必要在原始QEq方案中使电负性成为电荷本身的函数。因此，电荷的解决方案现在需要一个迭代的自洽过程。在这里，从Rappe和Goddard的公式中提出了一个修改后的公式，该公式极大地简化了分析导数的计算：

简化的原因是基于赫尔曼-费曼定理，可以理解如下。考虑可变电荷能量的笛卡尔一阶导数：

其中第一项表示传统的固定电荷导数，第二项是电荷变化作为结构函数的贡献。然而，如果选择每个几何体的电荷以使体系的总能量最小化，那么关于电荷的内能的一阶导数为零，因此校正消失。因此，在计算二阶导数矩阵时，只需要评估电荷相对于位置的一阶导数。