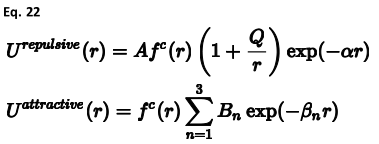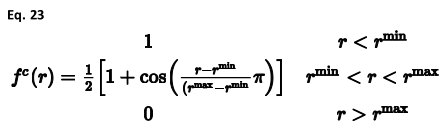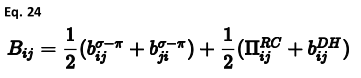4.6键级势能

在许多方面与嵌入原子方法有关，但有一个更复杂的形式，即所谓的键级势。人们认识到，局部结合能可以表示如下：

其中Bij是原子i和j之间的键序。键序取决于两个原子的局部环境，从而将明显的两体相互作用转化为多体已经提出了几种不同的公式，最著名的是Tersoff（1986和1988），以及最近的Pettifor等人（2002），后者对键序的贡献进行了更广泛的分析，并利用第一性原理方法来提取参数。近年来，一个特定的模型由于其对碳多晶型物和碳氢化合物体系的适用性而产生了巨大的影响，这是由于Brenner（1990）。这种势能已被广泛应用于富勒烯、纳米管和金刚石。在GULP中独立实现了Brenner模型，因为该程序的功能要求存在至少二阶，最好是三阶的分析导数。迄今为止，已有三种已发表的布伦纳势变体，但只有这些模型中的最新模型（Brenner等人，2002）在GULP中实现，因为它取代了前两个。布伦纳模型中能量的表达式中的项表示如下：

其中A、Q、α、B1-3和β1-3是参数化常数，取决于所涉及的原子种类C或H，fc（r）是余弦锥函数，以确保势能平稳地变为零：

键序条款本身由几个条款组成：

请注意，由于第二个术语的因子为一半，Bij的上述表达式与定义手稿中给出的表达式不同，但需要获得与引用的结果一致的结果。上述方程中的前两项分别表示原子i和j的局部键长和角度的影响，而第三项是对自由基性质的校正，第四项是二面角的影响。最后两个术语都与存在的共轭程度有关。这些术语的完整定义方程以及参数可以在原始参考文献和随后的勘误表中找到。

在以上对键序的多体贡献中，双三次和三次样条用于插值参数值。对于分布式布伦纳势能码，样条曲线系数是预先计算的，并作为数据文件提供。在本实施方式中，样条曲线是在内部动态执行的。这具有两个优点，即既避免了可能的转录错误，也避免了输入/输出造成的精度损失，并允许容易地实现参数拟合的可能性。

由于Brenner势的短程性质，在GULP中实现了两种不同的相互作用评估算法。第一种是对所有原子进行常规搜索，以找到具有非零相互作用的邻居。第二种方法是将体系空间分解为边长等于势能最大范围的立方体。因此，只有相邻立方体中的原子才能相互作用。这导致了线性缩放算法，该算法对于大型体系而言效率高得多。

虽然布伦纳模型确实有很多优点，比如它描述键离解的能力，但也有一些局限性。也许最重要的是描述远程力的困难。例如，石墨片之间没有粘合。已经提出了许多补救措施，包括增加两体势能来描述这些效应，要么只在不同分子之间，要么通过锥形来消除短距离的相互作用，以免使参数化无效。然而，这些方法也有局限性，尽管在Brenner势能导致的现有相互作用显著的情况下，去除远程力的贡献的更复杂的表达式显示出了希望（Che等人，1999）。到目前为止，这种方法还没有在GULP中实现。