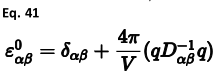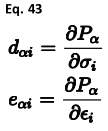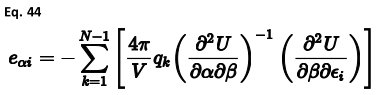4.9晶格性质

对于优化的本体结构，可以计算关于内部应变和外部应变的二阶导数。然后可以导出作为二阶导数函数的一些性质，这些属性在描述晶格对不同类型扰动的响应方面起着重要作用。

4.9.1介电常数

材料的介电性质在许多情况下都至关重要，包括那些超出严格体性质的情况。例如，固体对带电缺陷的响应取决于介电常数的倒数。介电常数的实际值根据所施加的电磁场的频率而变化。通常会引用两个极值，即静态介电常数和高频介电常数。在静态极限下，晶体的所有自由度，包括核自由度和电子自由度，都能够对电场做出响应，从而提供屏蔽。

在高频极限下，振荡大于材料的最大振动频率，因此，只有电子能够足够快地响应微扰。这里，描述这些极值的计算，而中频的情况将在后面介绍。

静态介电常数（3×3）张量可以由所有粒子的笛卡尔二阶导数矩阵Dαβ和包含所有粒子电荷的向量q确定：

其中α和β是笛卡尔方向。

高频介电常数的表达式与静态等效的表达式相同，只是二阶导数矩阵Dαβ现在只包括模型中任何壳体的笛卡尔分量。如果使用仅核心模型，那么高频介电张量只是一个单位矩阵。因此，由于相对直接的相关性，关于高频介电常数的信息在确定壳模型的参数时特别有用。

由于介电常数张量取决于反二阶导数矩阵，它具有Hessian矩阵的许多特征，因此，它是势能模型是否合理的一个非常敏感的指标。极值，尤其是负值，会立即指出势能模型不足或体系希望发生对称性变化的事实。

4.9.2折射率

材料的折射率n简单地与介电常数相关：

对于正交晶胞、四方晶胞或立方晶胞，在标准方向上，这表示一个平凡的映射，因为介电常数张量是一个对角矩阵，因此可以直接取平方根。对于其他晶体体系，有必要首先对张量进行对角化，然后在这个新的轴本征体系中找到折射率。

4.9.3压电常数

压电常数是许多技术应用中的关键量，因为它们控制着材料中的应变与非中心对称材料施加的电场之间的相关性（中心对称材料的所有压电常数必须为零）。压电常数也有几种不同的类型，这取决于所考虑的是由给定应变引起的极化，还是由施加的电场引起的应力/应变。在GULP中，计算压电应力常数d和压电应变常数e：

根据方向，这两个集合通过涉及弹性常数或弹性柔度张量的变换相关联。压电应变常数由笛卡尔二阶导数矩阵根据以下公式计算：

通过乘以弹性柔度张量，可以容易地将上述压电应变常数转换为压电应力常数。