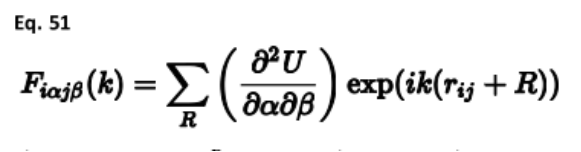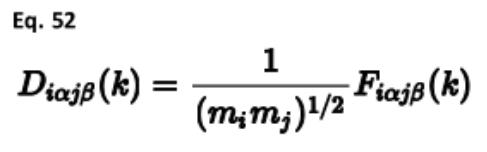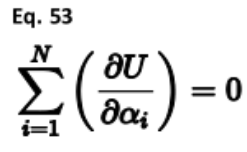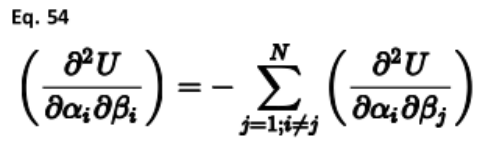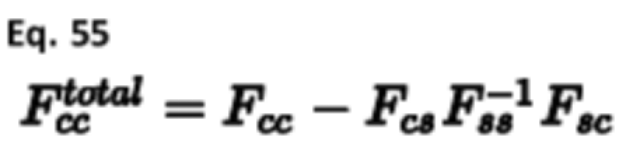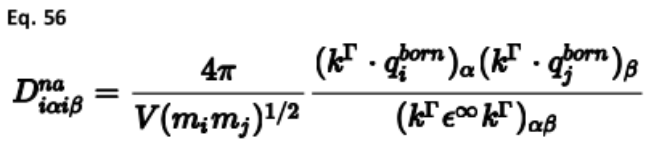4.12声子-4.12.1声子模的计算

由于海森堡不确定性原理，原子必须不断运动，这是通过振动实现的。在低温下，振动对应于围绕最小能量位置的简谐运动，而随着温度的升高，它们变得越来越不和谐。对于一个分子，会有3N-6个振动模式（对于线性体系，则为3N-5个）。在无限完美的三维固体的情况下，会有相应的无限数量的声子。这些声子是通过计算倒数空间中的点的值来描述的，通常在第一布里渊区内。因此，每个k点可以获得3N个声子。最低的三种模式代表所谓的声学分支，在布里渊区（k=0，0，0）的中心，即Γ点，其值往往为零。在这一点上，声学模式对应于晶格的纯平移，因此，它们是零频率的模式。振动频率与k的关系图产生了声子色散曲线。

为了计算体系的振动或声子，起点是力常数矩阵，由笛卡尔空间中原子的二阶导数给出。在固体的情况下，这些项必须乘以相应的相位因子exp（ik·r）。因此，两个原子i和j之间的力常数矩阵F由下式给出：

R上的总和表示截止半径内晶格矢量上的总和。然后，通过乘以离子的平方根质量倒数，将力常数矩阵转换为动力学矩阵D：

固体的Γ点或分子的规则振动光谱中的三个声学声子的起源，源于控制能量导数的和规则。首先，在没有外力的情况下，所有一阶导数或力的总和必须等于零：

其次，通过进一步微分上述表达式，可以表明力常数矩阵的对角线上元素等于非对角线元素的负和：

其中求和现在排除了i=j的情况。应该注意的是，如果使用两区域策略对表面进行声子计算，那么在区域中心将不再存在零频率的三种模式。这是因为区域2的影响起到了外力的作用，打破了平移不变性。

在由力常数矩阵形成动力学矩阵时，存在许多与特定力场和体系类型有关的问题。最常见的问题与壳层模型的使用有关，在壳层模型中，壳层的质量为零。由于振动模式的数量严格由原子数量的三倍给出，在这种情况下，原子数量也对应于核的数量，因此壳层坐标不能直接出现在动力学矩阵中。相反，根据以下表达式，将壳的贡献计入堆芯的力常数：

其中Fcc、Fss和Fsc分别是核心、壳-壳和壳-芯力常数矩阵，Fcs只是Fsc的转置。在呼吸式壳体模型的情况下，壳体指数被扩展到壳体半径及其笛卡尔坐标上。

在Γ点，声子的计算有一个额外的复杂性。在原子具有电荷的材料中，由于振动过程中产生的电场模式下的横向光学（TO）和纵向光学（LO）的简并性被破坏。这种影响在动力矩阵的通常分析评估中是不允许的。此外，发生的精确分裂也取决于在倒数空间中接近Γ-点的方向，kΓ-（也就是说，在声子色散图中，LO和to模式可能在这一点上是不连续的）。如果已知Born有效电荷，则可以通过对动力学矩阵添加校正来校正该非分析项（Cochran和Cowley，1962）（Baroni等人，2001）：

正如可以预期的那样，电荷对LO-TO分裂的影响是以与高频介电常数张量成反比的方式介导的。

关于Γ-点声子的计算，出现了两种情况。如果需要特定接近方向的值，例如在声子色散曲线的情况下，则可以明确指定kΓ的值。当Γ-点是GULP中的一个点的一部分时，接近的方向被自动设置为等于声子色散曲线的方向。或者，如果打算将红外光谱计算为多晶平均值，那么此时的声子在所有可能的方向上都应该是球形平均值。为了考虑到最后一种可能性，GULP有可能通过在球面极坐标中对作为θ和ξ函数的声子模式进行采样，然后对所得频率进行平均来进行数值积分。