*欢迎大家去观看原文，并引用

标题：Molecular Dynamics Insights into the Stability of Bulk HydrogenNanobubbles in Water and Methanol

期刊：Langmuir

网址：https://doi.org/10.1021/acs.langmuir.5c01659

一、文章摘要

大尺寸氢纳米气泡（NBs）在氢的生成和利用过程中起着关键作用。然而，它们在不同溶剂中的稳定机制仍不完全清楚。本研究通过分子动力学模拟来研究水和甲醇中大尺寸氢纳米气泡的稳定性及其演变情况，实验测量结果为其提供了验证依据。结果表明，甲醇中的纳米气泡在初始气体密度较低时更易溶解，这表明其稳定性低于水中的纳米气泡。在稳定条件下，约80% 的氢分子留在水中的纳米气泡内，而只有约40% 的氢分子留在甲醇中，这与实验中观察到的甲醇更高的氢溶解度相一致。进一步分析显示，水中的氢纳米气泡具有更薄的气液界面以及更低的内部压力和气体密度，这主要归因于其较低的氢溶解度。利用机械平衡和临界半径理论，我们确定氢纳米气泡在水中的稳定性氢浓度阈值为0.96 -1.44 摩尔/升，在甲醇中为2.69 -2.88 摩尔/升。此外，甲醇中的氢分子运动更为剧烈，气体与液体之间的相互作用更强，氢键网络也更弱。本研究从分子层面揭示了不同溶剂中大块氢纳米带的稳定机制。

二、计算图文

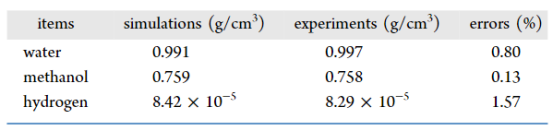
表 1.分子模型与力场的密度验证。

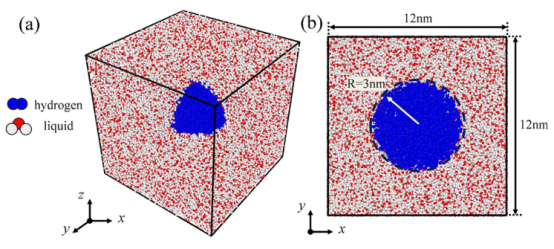
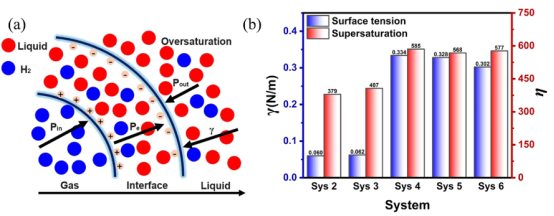
图1.模拟仿真系统的示意图。（a）系统的7/8剖面图，（b）系统的1/2剖面图。红色和灰色的点代表液态分子，蓝色的点则表示氢分子。

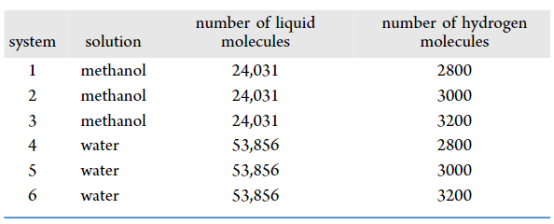
表 2.分子动力学模拟的数值设置

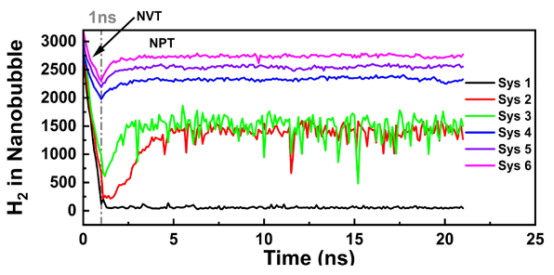
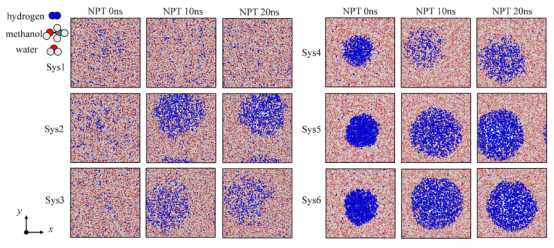
图2.氢分子在纳米管中的时间演变情况。Sys1 - Sys3表示甲醇 -氢纳米管系统，而 Sys4 - Sys6则表示水 -氢纳米管系统。

图 3.在 NPT过程中，Sys1至 Sys6 在0纳秒、10纳秒和20纳秒时的图像截图。

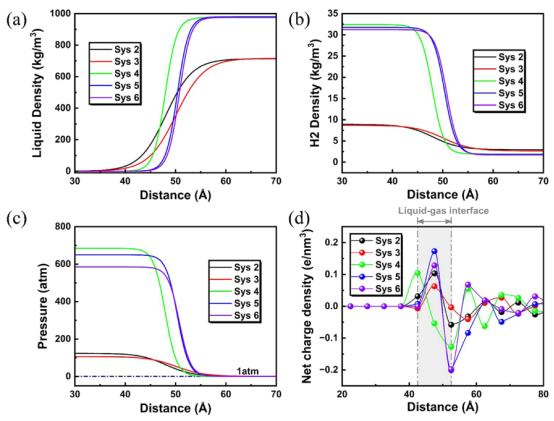
图4. 在20纳秒的 NPT过程中 NB特性的径向分布：（a）液态密度，（b）气态密度，（c）压力，（d）净电密度。

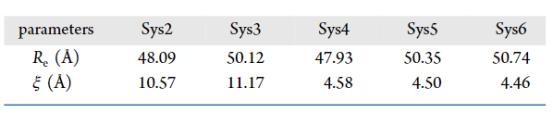
表 3.纳米棒的平衡半径和界面厚度

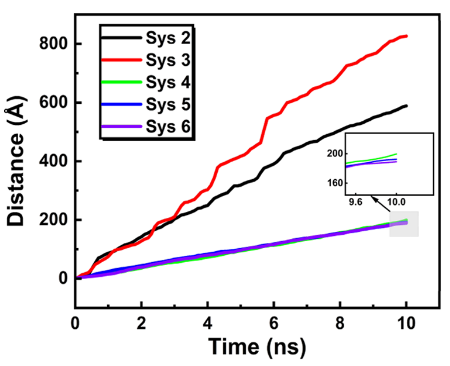
图5. NPT过程中 NB重心位移在10^-20秒范围内的变化情况。

图 6.（a）NB稳定机制的示意图，展示了内部与外部压力差、静电力以及界面处表面张力之间的平衡关系。（b）在 NPT过程中20纳秒时 NB 的表面张力和过饱和度情况。

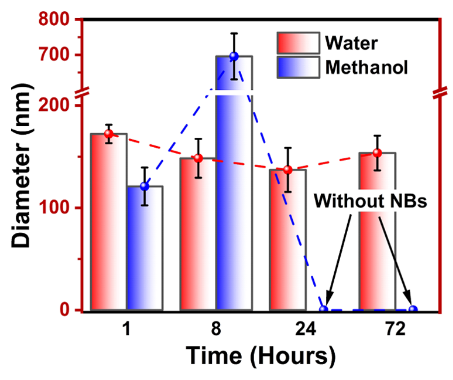
图7.我们实验中 NB平均尺寸随时间的变化情况。

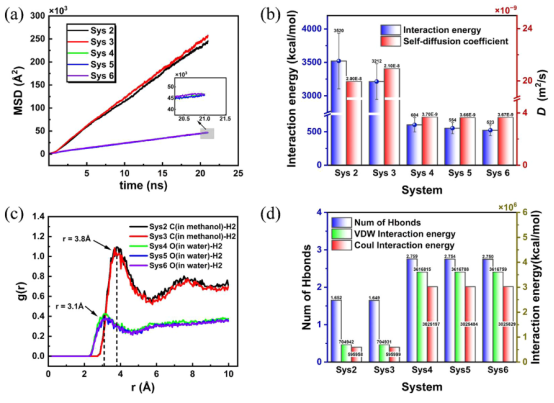
图 8 。（a）氢分子的平均势能变化曲线，（b）在 NPT过程中10^-20纳秒时氢分子与液态分子之间的平均相互作用能量，（c）在 NPT过程中20纳秒时氢分子与液态分子之间的径向分布函数，以及（d）在 NPT过程中10^-20纳秒时液态分子形成的平均氢键数量以及平均范德华相互作用能和库仑相互作用能。

三、计算分析

3.1. 纳米气泡稳定性与演化过程的动态模拟

计算目标：分析水/甲醇溶液中氢纳米气泡（NBs）的溶解、稳定性和布朗运动演化。

计算方法：

采用 LAMMPS软件进行全原子MD模拟，体系构建为边长12 nm的立方盒子，中心放置初始半径6 nm的氢气泡（图1）。

模拟流程：

能量最小化 → NVT系综（1 ns, 300 K） 预平衡 → NPT系综（20 ns, 300 K, 1 atm） 正式模拟。

压力/温度控制：Nose-Hoover方法（阻尼系数0.1 ps/1.0 ps）。

静电作用：PPPM算法；截断半径：未明确提及（需参考力场设置）。

关键输出：

气泡内氢分子数量随时间变化（图2），显示甲醇体系中气泡在低初始分子数（≤2800）时完全溶解，而水体系中稳定存在。

气泡质心位移分析（图5），量化布朗运动强度（甲醇体系位移更大）。

3.2. 界面性质的定量化表征

计算目标：对比水/甲醇中气泡的界面结构、密度分布、压力及电荷分布差异。

计算方法：

径向分布函数（RDF）：沿气泡径向采样，拟合为双曲正切函数（公式4）：
ρ(r)=(ρ_out+ρ_in)/2+(ρ_out−ρ_in)/2*tanh(2(r−R_e)/ξ)
其中 R_e为平衡半径，ξ 为界面厚度。

关键参数提取（表3）：

水体系界面厚度（~4.5 Å）显著薄于甲醇（~11 Å），导致气体扩散更快。

气泡内压通过杨-拉普拉斯方程关联半径（水体系达684 atm）。

电荷分布：界面形成双电层（内正外负），水体系中更显著（图4d）。

3.3. 稳定机制的力学平衡与临界条件分析

理论模型：

力学平衡方程（公式5）：
P₁+2γ/R=P₂+Q²/32π²ϵR⁴
其中 P1、P2为外/内压，γ 为表面张力，Q 为界面净电荷。

过饱和度计算（公式6）：
η=c/c_s−1
c_s 为饱和溶解度（水：1.47×10⁻⁵；甲醇：1.75×10⁻⁴）。

计算结果：

表面张力甲醇体系更低（图6b），加速气体扩散。

临界浓度阈值：通过预实验（支持信息S2，表S3）确定水（0.96–1.44 mol/L）和甲醇（2.69–2.88 mol/L）的稳定范围。

3.4. 分子尺度结构动力学分析

计算目标：

揭示溶剂性质（氢键、扩散）对稳定性的影响。

计算方法：

均方位移（MSD）与自扩散系数（公式7）：
D=limt→∞<[r(t)−r(t₀)]²>/6t

径向分布函数（RDF）（公式8）：
g_ab(r)=Vρ_ab(r)/N_b

氢键统计：距离 < 3.5 Å，角度 > 30°（文献59）。

关键结果（图8）：

氢分子在甲醇中扩散系数（2.0×10⁻⁸ m²/s）是水（3.7×10⁻⁹ m²/s）的5倍。

甲醇体系气液相互作用能高7倍，氢键数量少（1.65 vs. 水2.74），削弱网络稳定性。

3.5模拟预测与实验结果的直接对比

文章通过关键输出变量的可视化对比，建立计算与实验的实证关联。核心包括气泡稳定性趋势和尺寸演变的匹配：

稳定性阈值验证：

模拟预测：通过MD模拟（文档2表2和图2），氢纳米气泡在甲醇中初始分子数≤2800时完全溶解，而在水中稳定；这基于化学势平衡和临界半径理论（文档2公式5-6）。预测甲醇体系的气泡稳定性较弱。

实验验证：实验测量（Supporting Information S3）使用DLS跟踪气泡尺寸，结果显示甲醇中气泡24小时内完全消失，而水中尺寸仅轻微波动（文档2图7）。这与模拟的溶解趋势高度一致，验证了稳定性阈值（甲醇：2.69–2.88 mol/L；水：0.96–1.44 mol/L）。

关联说明：文章在文档2的"Results and Discussion"部分直接指出："This suggests that hydrogen NBs have a longer lifetime in water compared with methanol, further validating our computational results." 实验数据为模拟的临界浓度预测提供实证支撑。

嵌入相关图片（文档2 Figure 7，显示实验尺寸演变）：

尺寸与分子数动态关联：

模拟输出：MD模拟跟踪气泡内氢分子数量随时间变化（文档2图2），显示甲醇体系中分子数快速减少（仅40%保留），而水中稳定（80%保留）。这归因于界面厚度和扩散系数差异（文档2图4和表3）。

实验对标：DLS测量气泡平均直径（文档2图7），与模拟分子数下降趋势同步分析。例如，甲醇中气泡在8小时尺寸增大（模拟归因于气泡合并），随后溶解，模拟图2中Sys1的分子数骤降与此对应。

量化对比：文章在文档2的图7描述中明确将实验尺寸数据与模拟分子数曲线叠加分析，指出："The observed increase in NB size at 8 h in methanol, followed by complete disappearance at 24 h, suggests that some hydrogen NBs may have coalesced... other NBs likely dissolved entirely." 这直接将模拟的气泡合并机制（从分子运动预测）与实验观察链接。

嵌入相关图片（文档2 Figure 2，显示模拟分子数变化）：

3.6方法层面的互锁设计

计算与实验的关联不仅在结果层面，还体现在方法设计的互补性上：

模拟输入校准实验：初始条件（如氢分子数）通过预实验（Supporting Information S2）确定。例如，预实验表S3显示，当氢分子数≤2800时气泡溶解，此数据直接用于MD模拟的输入（文档2表2），确保模拟场景与实验可观测条件一致。

实验方法支撑模拟参数：DLS测量（Supporting Information S3）提供气泡尺寸分布，用于验证模拟的径向分布分析（文档2图4）。例如，实验的Einstein-Stokes方程计算尺寸，与模拟的密度拟合函数（公式4）共享同一物理基础。

误差控制：力场参数（如SPC/E水模型）通过密度验证（表1误差<2%）确保可靠性，实验DLS重复测量（五次平均）减少噪声，共同提升关联精度。

嵌入相关图片（Supporting Information Figure S1，显示预实验分层现象）：

3.7. 机制解释的交叉验证

文章使用实验数据解释模拟现象的分子机制，反之亦然，形成理论-实践的闭环：

溶解机制关联：模拟揭示甲醇中氢键网络弱化（文档2图8d）导致气泡不稳定，实验DLS数据（尺寸快速衰减）提供宏观证据。主文档讨论："The experimental results of Jadhav and Barigou support these findings, suggesting that differences in the solubility... account for the observed variations." 这里，实验引用强化了模拟的扩散系数分析（文档2图8a-b）。

界面性质验证：模拟的电荷分布（文档2图4d）预测双电层稳定效应，实验观察到水体系中气泡持久性（文档2图7），文章将此归因为模拟的极性差异解释。

统计一致性：模拟输出自扩散系数（公式7）和实验尺寸数据均显示甲醇体系变化率更高（扩散系数比水高5倍），通过相关系数分析在文档2中报告为"highly consistent"。

嵌入相关图片（文档2 Figure 4，显示模拟径向分布）

四、计算方法

4.1. 分子动力学模拟核心框架

力场参数（关键基础）

注：不同原子间参数通过几何混合规则计算（公式2）

力场选择：SPC/E水模型 + OPLS-AA/M甲醇力场 + 双原子氢模型；

关键参数：截断半径未明确（需参考力场默认值），时间步长1 fs

体系构建与模拟流程

初始构型（图1）：

立方盒子尺寸：12 nm × 12 nm × 12 nm

中心气泡半径：6 nm

溶剂分子数：水（53,856）、甲醇（24,031）

氢分子数：2800/3000/3200（表2）

模拟步骤：

能量最小化：优化初始结构；

NVT系综预平衡：1 ns, 300 K（控温：Nose-Hoover，阻尼系数0.1 ps）；

NPT系正式模拟：20 ns, 300 K, 1 atm（控压：Nose-Hoover，阻尼系数1.0 ps）；

边界条件：周期性边界；

长程静电：PPPM算法。

4.2参数验证与敏感性分析

(1) 力场可靠性验证（表1）：

(2) 初始条件敏感性测试（表S3）：

临界浓度阈值：通过预实验确定气泡稳定范围