|
天然橡胶与聚丁二烯界面处热传输特性的分子动力学研究
*欢迎大家去观看原文,并引用 标题:Molecular Dynamics Study on the Thermal Transport Properties atthe Interface of Natural Rubber and Polybutadiene 期刊:Langmuir 网址:https://doi.org/10.1021/acs.langmuir.5c01331
一、文章摘要温度和压力在橡胶的热导率以及不同橡胶材料之间的界面热传递方面起着至关重要的作用。在本研究中,通过分子动力学模拟来探究在不同温度和压力条件下天然橡胶(NR)和聚丁二烯(PB)的热导率,以及它们的界面热传递特性。结果表明,橡胶的热导率随温度升高而增加,而压力对这一影响并不显著。当温度从200 K升高到400 K时,NR 和 PB之间的界面厚度增加了286.54%,界面热阻增加了7.85倍。然而,压力对界面热阻的影响并非呈线性趋势。因此,温度被认定为影响橡胶材料热传输的关键因素。这些发现为橡胶材料在热管理方面的应用提供了重要的理论指导。
二、计算图文
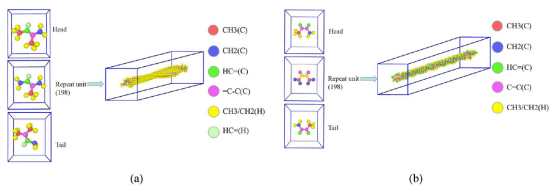
图 1.(a)聚合度为200 的 NR单链,(b)聚合度为200 的 PB单链。
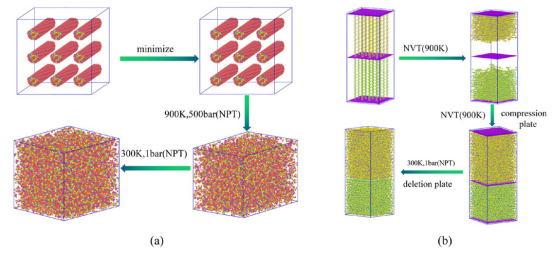
图 2.(a)单个系统的弛豫过程,(b)单个界面系统的弛豫过程。
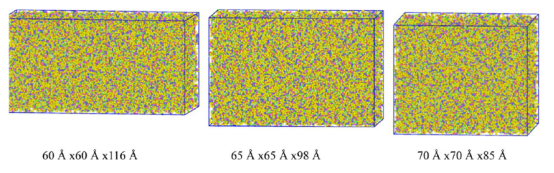
图 3.不同规格的系统。
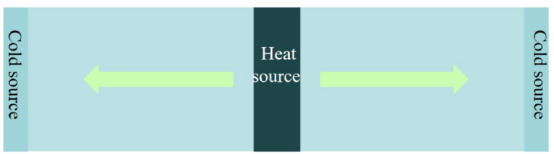
图 4.冷热源的分布情况。
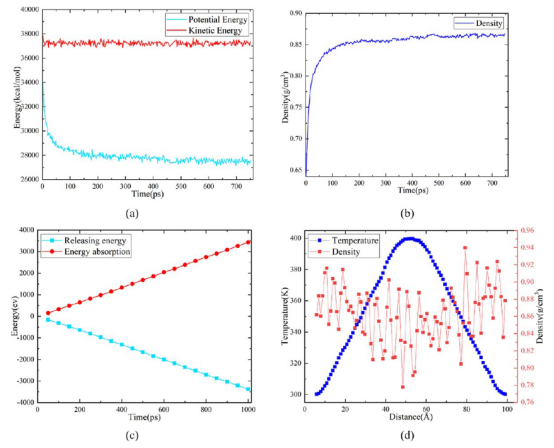
图 5.(a)能量变化图,(b)密度变化图,(c)能量分布图,(d)热传递方向上的温度分布图。
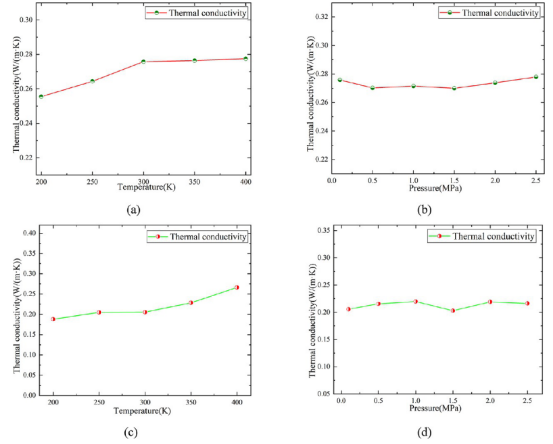
图 6.(a)丁腈橡胶在不同温度下的热导率,(b)丁腈橡胶在不同压力下的热导率,(c)丁二烯橡胶在不同温度下的热导率,(d)丁二烯橡胶在不同压力下的热导率。
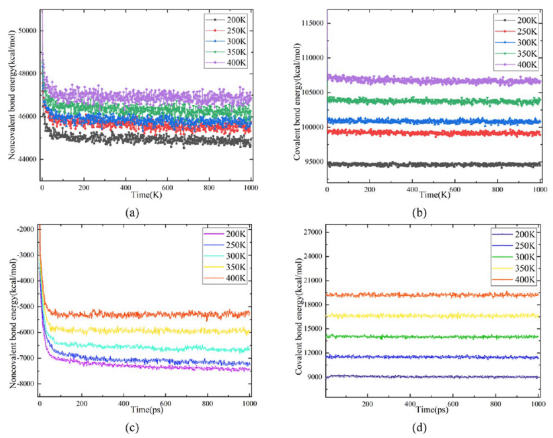
图 7.(a)NR 在不同温度下的非共价键能,(b)NR 在不同温度下的共价键能,(c)PB 在不同温度下的非共价键能,(d)PB 在不同温度下的非共价键能。
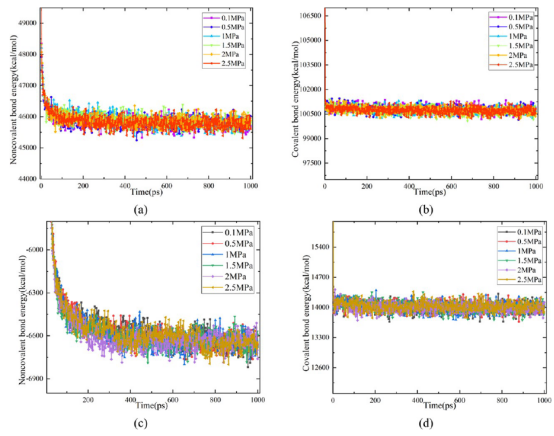
图 8 。(a)不同压力下 NR 的非共价键能,(b)不同压力下 NR 的共价键能,(c)不同压力下 PB 的非共价键能,(d)不同压力下 PB 的非共价键能。
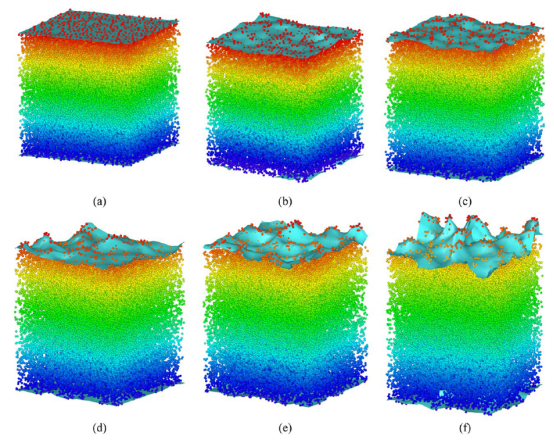
图 9 。当压力 P =0.1兆帕时,NR 和 PB 在不同温度下的界面形状,(a)初始界面,(b)200 K时,(c)250 K时,(d)300 K时,(e)350 K时,(f)400 K时。
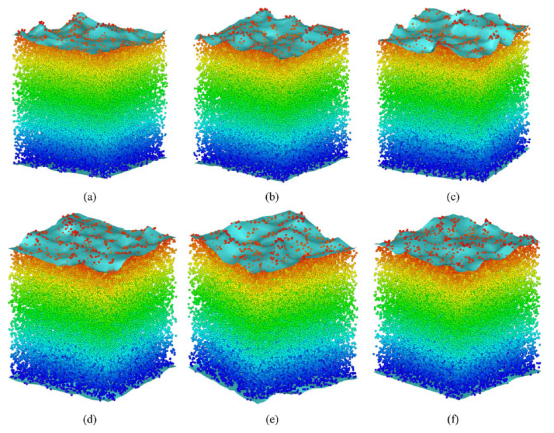
图 10.在温度为300 K时,不同压力下 NR 和 PB 的界面形状,(a)0.1 MPa,(b)0.5 MPa,(c)1 MPa,(d)1.5 MPa,(e)2 MPa,(f)2.5 MPa。
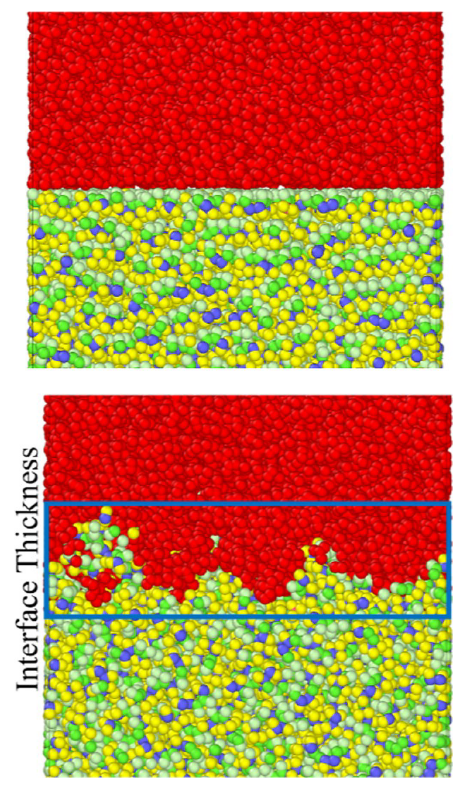
图11.界面厚度示意图。
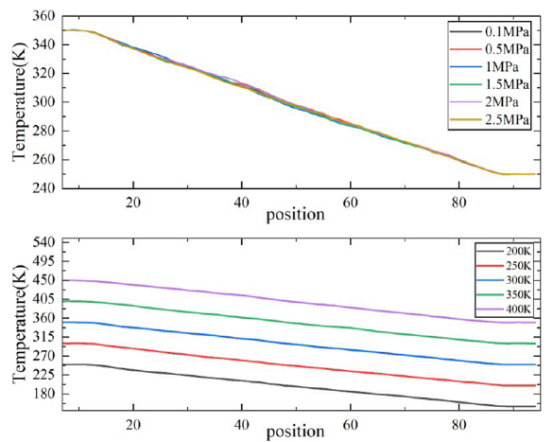
图 12.沿热传递方向的温度分布。
三、计算分析3.1热导率温度/压力依赖性模拟了天然橡胶(NR)和聚丁二烯(PB)在 200–400 K和 0.1–2.5 MPa下的热导率(图6)。
关键结论: 热导率随温度升高而显著增加(NR:0.2758 W/(m·K) @300 K;PB:0.1881 W/(m·K) @300 K)。 压力对热导率无显著影响(非线性关系)。
3.2能量传递微观机制量化了共价键能(键能、角能、二面体能)与非共价键能(范德华力)随温度/压力的变化(图7, 图8)。 关键机制: 温度升高增强分子链振动和非共价相互作用,促进能量传递(图7a-d)。 压力对能量分布无显著影响(图8a-d)。
3.3界面热传输特性分析了NR/PB界面厚度(图9-10, 图13)和界面热阻(图14, 表2-3)。 关键发现: 温度从200 K升至400 K → 界面厚度增加286.54%(图13a)。 界面热阻随温度升高增加7.85倍(表2),压力影响非线性(表3)。
3.4热导率数据的实验对标1. 关键数值直接对比在300 K条件下,模拟结果明确标注与实验值的匹配性: NR热导率:模拟值 0.2758 W/(m·K)≈ 实验值(未给出具体值,但强调 "in close agreement with experimental results") PB热导率:模拟值 0.1881 W/(m·K)≈ 实验值 差异解释:引用文献数据说明方法依赖性(如Chen用NEMD得0.178 W/(m·K),He用EMD得8.76 W/(m·K)),强调本文采用 NEMD方法的合理性(见原文第3节)。
2. 温度趋势的实验支撑模拟显示热导率随温度升高而增加(图6a,c),与文献中 环氧树脂的实验规律一致("consistent with the findings of this study")。 对比 PTFE的模拟研究(热导率随温度下降),突显橡胶材料的特殊性。
3.5微观机制的物理解释1. 能量传递机制验证通过分析 共价键能和 非共价键能(图7-8),解释温度升高提升热导率的原因: "温度升高增强非共价相互作用(范德华力),促进能量传递" 该结论与实验观测的聚合物热导率温度依赖性一致(如文献12中拉伸聚合物链增强热导率的实验)。
2. 界面行为的实验关联界面厚度增长286%(200 K→400 K)与 界面热阻增加7.85倍的模拟结果(图13-14),为实验中高温下橡胶复合材料界面脱粘现象提供微观解释。 引用 纳米填料掺杂实验(文献22)佐证界面调控的重要性(见结论部分应用建议)。
3.6模拟方法的实验校准1. 力场与参数的实验校准采用 OPLS-AA力场(文献16),其参数源自有机分子实验数据,确保原子相互作用可靠性。 弛豫判据依据能量/密度平衡(图5a-b),与聚合物玻璃化转变的DSC实验特征吻合。
2. 尺寸效应验证通过多尺寸体系测试(图3及表1),确认热导率波动<5%,排除有限尺寸效应: 该流程参照文献6-8中聚合物热导率模拟的标准验证方法。
3.7差异分析与应用衔接1. 压力效应的特殊性
模拟发现压力对热导率影响不显著(图6b,d),而实验文献中压力常通过改变自由体积影响热导率。作者归因于: "橡胶的高分子链柔性减弱压力对结构的扰动" 该解释与橡胶的 超弹性实验行为一致(如文献2中橡胶的压缩模量测试)。
2. 应用导向的转化设计基于模拟结论提出三项实验应用方案:
四、计算方法4.1分子动力学模拟核心方法1. 模型构建流程
2. 力场与边界条件
关键验证:测试不同体系尺寸(图3)和时间步长(表1),确认结果波动<5%
表1 体系尺寸与时间步长敏感性验证
4.2热导率计算(非平衡分子动力学, NEMD)1. 热流生成与测量
2. 温度梯度与热导率计算温度梯度提取: ∇T=∂T/∂X(X:热传递方向位置)
傅里叶定律计算: λ=J/(∇T⋅A)(A:截面积)
平衡判据: • NVE系综平衡1.5 ns • 验证温度分布线性(图5d)与能量稳定(图5c)
4.3界面热传输参数化分析1. 界面厚度与形貌表征
2. 界面热阻计算R=JΔT(单位:m2⋅K/W) ΔT:界面区温度跃变值(图11) J:热流密度(同公式1) 数据输出示例(表2节选):
4.4能量作用机制分析能量分解参数
|