|
通俗讲解:相空间体积元时间:2025-05-15 相空间体积元是描述微观粒子运动状态的“多维微积分单元”。在由广义坐标(位置)和广义动量构成的相空间(一种高维抽象空间)中,体积元表示某一瞬间所有粒子可能状态的集合范围。
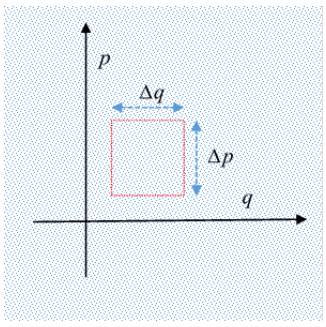
数学表示:若系统有N个粒子,每个粒子需要3个位置坐标和3个动量坐标,则相空间体积元为 dΩ=dq1dq2 ⋯dq3Ndp1dp2⋯dp3N。
通俗比喻:想象一个由无数个坐标轴组成的“超立方体”,每个坐标轴代表一个粒子的位置或动量,体积元就是这个立方体中的一个微小格子,用来标记所有粒子此刻的状态组合。
一、目的与科学意义相空间体积元的核心作用在于建立微观运动与宏观统计的桥梁:
统计物理基础:通过统计体积元内所有微观状态的出现概率,计算宏观量(如温度、压强)。 案例:计算气体的压强时,无需追踪每个分子的碰撞细节,只需统计动量分布的均值。
守恒定律支撑:根据刘维尔定理,相空间体积在演化过程中保持不变。 案例:墨水扩散时,虽然分子位置分布变广,但相空间体积不变(宏观熵增与微观守恒的统一)。
二、通俗案例解析场景:将一滴墨水滴入静水中,墨水逐渐扩散至整个容器。 相空间视角: 每个墨水分子的位置和动量构成6维坐标,初始时集中在相空间的小体积元内。 扩散过程中,体积元在相空间中“拉伸变形”,但总体积始终不变。 意义:看似无序的扩散,实则在更高维度遵循严格守恒,这正是热力学熵增的本质。
上一篇通俗讲解:刘维尔定理下一篇通俗讲解:遍历性假设 |