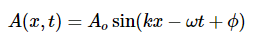2.1：一维波动方程

学习目标

引入波动方程，包括时间和位置依赖性

在最一般的意义上，波是具有波状特性和结构(存在波峰和波谷)的粒子或其他介质。

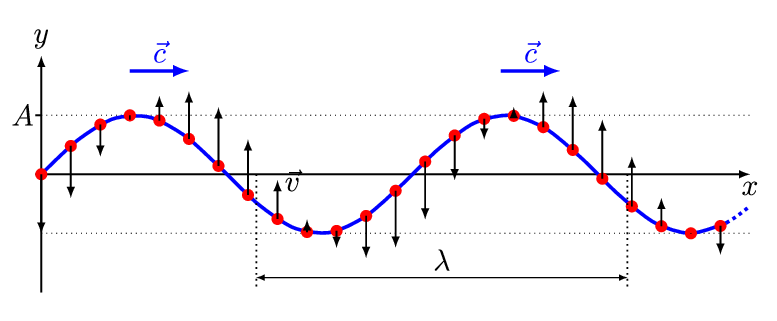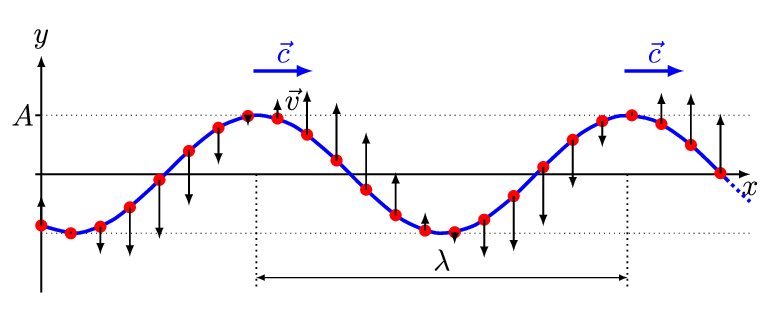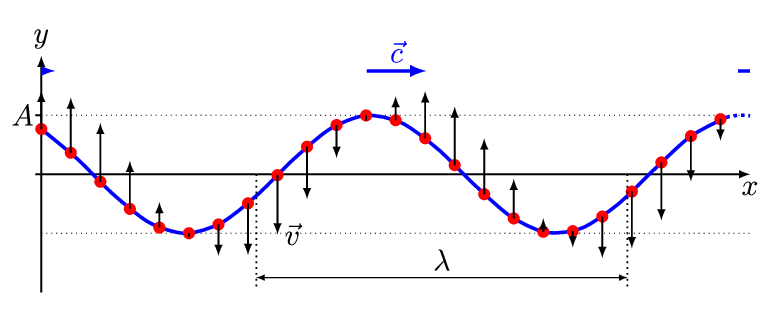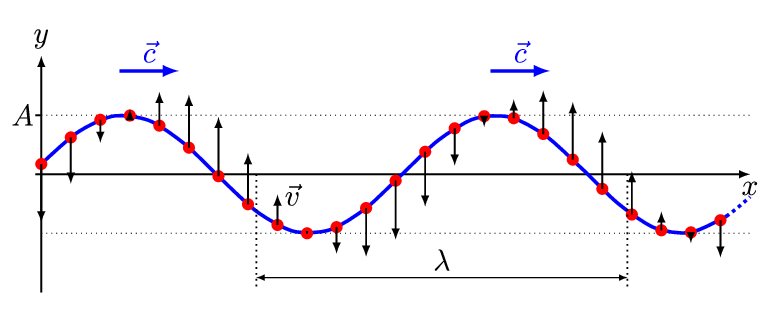
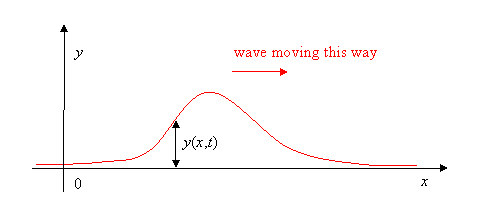
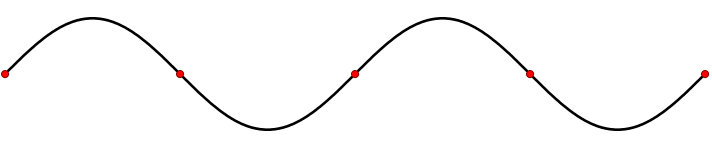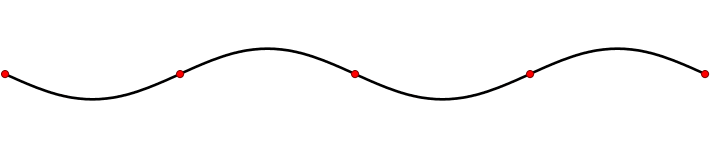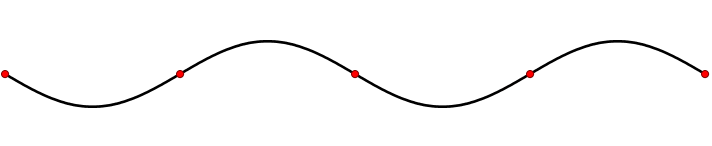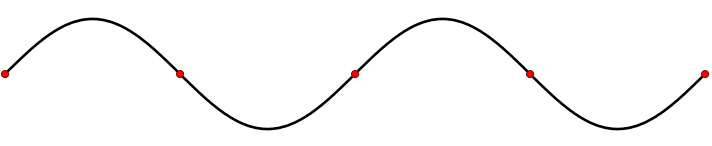
图2.1.1：简单的平移(横)波。

最简单的波是(空间上)一维正弦波(图2.1.1)，其幅度为变化A由方程式描述：

这里A_o是波的最大振幅，即在一个波周期内从介质中扰动的最高点(波峰)到平衡点的最大距离。在图2.1.1中，这是基线和波形之间的最大垂直距离。

x是空间坐标

t是时间坐标

k是波数

ω是角频率

φ是相位常数。

可以将“波”分为两组：行波和驻波。

行波

行波(例如海波或电磁辐射)是“移动”的波，这意味着它们具有频率并通过时间和空间传播。描述“波运动”这种特性的另一种方式是能量传输–波在设定的距离内传播或传输能量。日常生活中最重要的行波种类是电磁波、声波，也许还有水波，这取决于你住在哪里。很难分析在三个维度上传播的波、从物体上反射等，因此我们从最简单的有趣波示例开始，这些波仅限于沿线移动。让我们从一根绳子开始，就像晾衣绳一样，在两个钩子之间伸展。你把钩子的一端从钩子上取下来，握住绳子，保持它拉得相当紧，然后向上和向后挥动你的手一次。如果你做得足够快，你会看到一个沿着绳子移动的颠簸：

图2.1.2：某一时刻t的一维行波

这是行波的最简单示例。您可以通过以不同的模式上下移动手来制作不同形状的波浪，例如向上的碰撞后下降，或两个碰撞。您会发现行波在沿着绳索移动时保持相同的形状。将绳子拉得足够紧，以便我们可以将其水平，我们将它的静止位置作为我们的x轴(图2.1.1)。y轴轴取垂直向上，我们只在上下方向摆动绳子，所以实际上y(x，t)将是绳子在x处距离其静止位置有多远在时间t时 :如图2.1.2显示了绳索在某一时刻t的位置.

现在我们可以更精确地表达波“保持相同的形状”的观察结果。为了方便起见，取t=0即波峰通过x=0的时刻，我们在这里绘制绳子在t = 0和一些稍后的时间t的位置作为动画(图2.1.3)。用y(x,0)=f(x)表示第一个函数，那么第二个y(x，t)=f(x−vt)它与“形状相同”的功能相同，只是vt移动了，其中v是波速。

图2.1.3：一维行波随时间的变化。行波以固定速度将能量从一个点传播到另一个点v。

综上所述：通过上下抖动绳子的末端，使波沿绳子传播，从观察结果来看，波以恒定的速度传播，并保持其形状，因此在x处的任何水平位置上的绳子位移y在时间t时具有以下形式

我们忽略了摩擦效应-在真正的绳索中，凸起会随着它的移动而逐渐变小。

驻波

与行波相反，驻波或驻波保持恒定位置，波峰和波谷以固定的间隔出现。产生各种驻波的一种方法是在一组吉他或小提琴弦上拨动旋律。当一个人将手指放在琴弦的一部分上，然后用另一个手指拨动它时，就会产生驻波。这个问题的解决方案包括琴弦以正弦波模式振荡(图2.1.4)，两端没有振动。两端之间的一系列等距点也没有振动;这些“安静”的地方是节点。最大振荡的地方是波腹。

图2.1.4：静止介质中驻波的动画，带有标记的波节点(红色圆圈)。

束缚粒子与自由粒子以及行进波与驻留波

行波在时间和空间中表现出运动和传播，而驻波具有由节点分隔的固定间隔的波峰和波谷。“自由”粒子，如光电子效应中讨论的光电子，表现出类似行波的特性。相比之下，“束缚”波的电子将表现出类似驻波的特性。后者被用于玻尔原子，用于量化氢原子内结合的电子的角矩。

波动方程

一维波(行进和驻留)的数学描述可以表示为

带u是位置x处波的振幅以及时间t，和v是波速（图2.1.2 )。

公式2.1.2称为一维经典波动方程，是一个线性偏微分方程。它告诉我们位移u如何随时间变化。u可以随位置、时间和函数而变化。波动方程的解(u（x，t））是通过适当的积分技术获得的。可能不会令人惊讶的是，并非所有可能的波都能满足方程2.1.2而波必须同时满足初始条件和边界条件，即波是如何产生的以及弦的末端发生了什么。

例如，对于长度为L两端绷紧(图2.1.3)，边界条件为

和

对于所有t值正如预期的那样，不同的系统将有不同的边界条件，因此有不同的解决方案。

量化的数学起源

用于求解波动方程的初始条件和边界条件将导致“允许”波的限制，其存在方式类似于玻尔原子中的电子仅存在某些解。

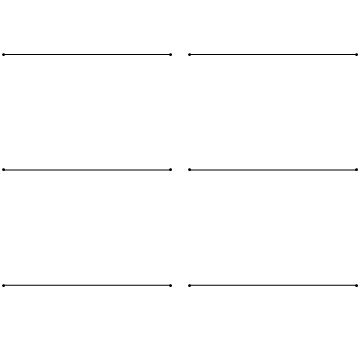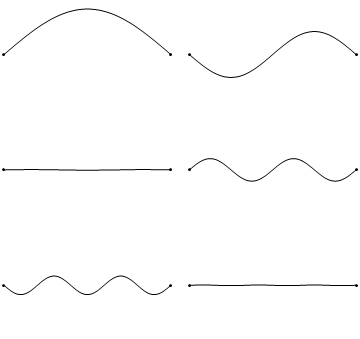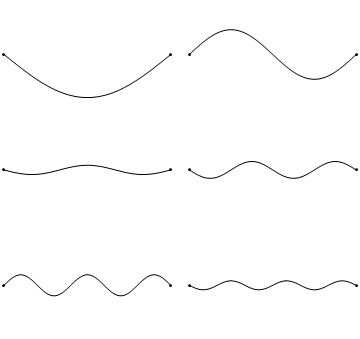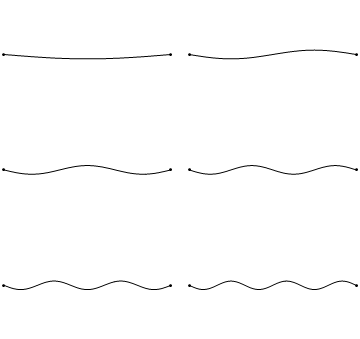
前六个波解u（x，t）见公式2.1.2受方程2.1.3中的边界条件限制以及2.1.4（稍后详细讨论）导致了图2.1.5中的波。这些是驻波，其频率基于它们所表现出的节点数（0、1、2、3……）（更多内容将在下一节中讨论）。

图2.1.5：字符串中的驻波(空间和时间)。前6个解决方案(u(x，t)

波浪曲率解

由于波幅的加速（方程2.1.2的右侧）与∂²/∂x²成正比材料的曲率越大，产生的加速度就越大，即波速变化越快（图2.1.4)，振荡频率也就越高。如后文所述，高频波（即节点更多）是能量更高的解；这与第一章讨论的实验结果一致，包括普朗克方程E=hν。..

总结

表现出运动并在时间和空间中传播的波。波的两种基本类型是行进波和静止波。两者都表现出波状特性和结构(存在波峰和波谷)，可以用波函数或振幅函数进行数学描述。两种波形类型都显示移动(上下位移)，但方式不同。行波具有波峰和波谷，当它们传播一段长度或距离时，它们会不断从一个点移动到另一个点。通过这种方式，能量沿着行波的长度传输。相比之下，驻波在固定位置有节点;这意味着波的波峰和波谷也位于固定的间隔内。因此，驻波仅在这些设定的间隔内经历振动运动(上下位移)——没有运动或能量沿着驻波的长度传播。