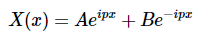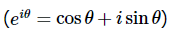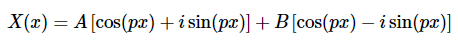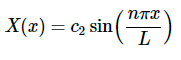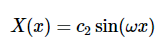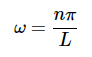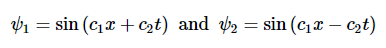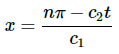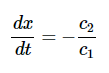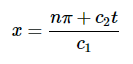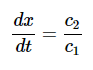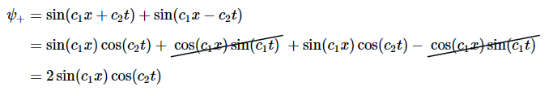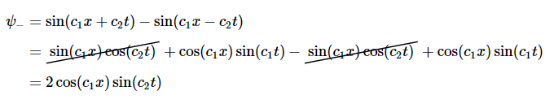|
2.3:微分方程的震荡解学习目标l 探索波动方程震荡解的基础 l 了解边界条件对可能解的影响 l 合理化满足边界条件如何强制量子化(即,仅存在具有特定波长的解)
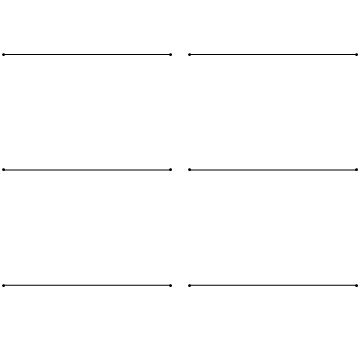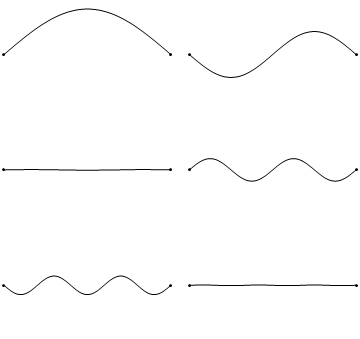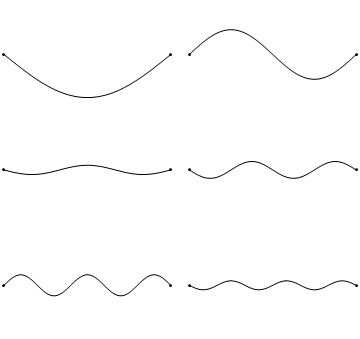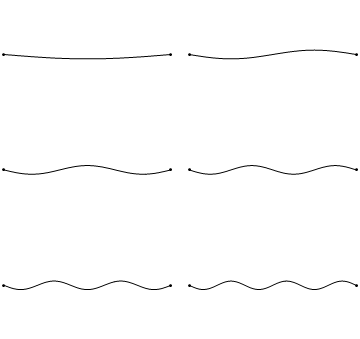
两端固定为零的弦的边界条件表明u(x,t)在弦的极端处坍缩到零(图2.3.1 )。
图 2.3.1 :字符串中的驻波(空间和时间)。
不幸的是,当K>0时,一般解(方程2.2.7)导致指数衰减和增长之和无法达到边界条件(除了平凡解);因此K<0,这意味着我们必须引入复数,因为√K方程2.2.5中的术语。因此,我们可以重写K:
方程 2.2.4b 可以表示为
方程2.3.2形式的微分方程的一般解是
例 2.3.1验证方程式2.3.3是方程2.3.2形式的微分方程的一般形式,其中用方程2.3.1代替交给
解答 通过欧拉公式
合并同类项
引入新的复数常量 c1=A+B和 c2=i(A−B)
因此,方程 2.3.4可以表示为振荡函数
现在,让我们应用方程2.2.7中的边界条件来确定常数c1。代入第一个边界条件(X(x=0)=0)代入方程2.3.5的通解,得到结果
并代入第二个边界条件(X(x=L)=0)代入方程2.3.5的通解,得到结果
我们已经知道c1=0从第一个边界条件得到方程2.3.7简化为
给定正弦的性质,方程 2.3.7 简化为
跟 n=0是我们忽略的无意义的解,因此 n=1,2,3...
代入公式2.3.10以及2.3.6代入公式2.3.5,得到结果
可以简化为
其中
类似的论点也适用于假设的另一半(T(t)). 练习 2.3.1给定两个行波:
求 ψ1 和 ψ2 找到以下内容并确定节点: ψ+=ψ1+ψ2和ψ−=ψ1−ψ2
解决方案 aψ1是一个正弦函数。在每个整数nπ处,其中n=0,±1,±2,...,正弦函数将为零。因此,当c1x+c2t=πn时ψ1=0。求解x,同时忽略无意义的解:
此波的速度为:
同样适用于ψ2。在每个整数nπ处,其中n=0,±1,±2,...,正弦函数将为零。因此,当c1x−c2t=πn时ψ2=0。解出x,对于ψ2:
此波的速度为:
每个波的波长是两个连续节点之间距离的两倍。换句话说,
解决方案 b找到 ψ+=ψ1+ψ2和ψ−=ψ1−ψ2
在每个x=nπ/c1处应有一个节点和
|