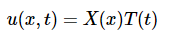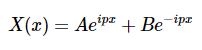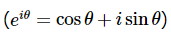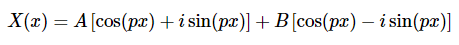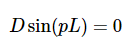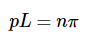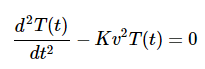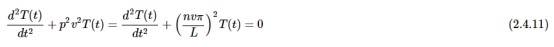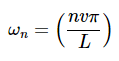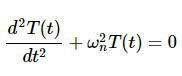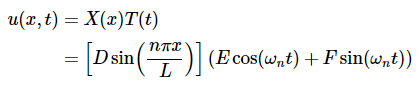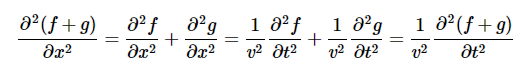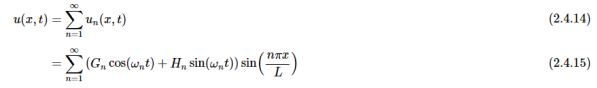2.4：通解是普通模式的叠加

学习目标

l 将波动方程分离为各个空间和时间问题并求解它们。

l 证明一般解可以是解的叠加(正则模态)

如前所述，求解u(x，t)对于所有x和t。假定它为X(x)以及T(t)两个函数的乘积，其中X(x)仅是x的函数，以及T(t)是t的函数。

通过将新的乘积解形式代入原始波动方程，可以得到两个常微分方程(包含一个自变量的一个或多个函数及其导数的微分方程)。每个微分方程只涉及一个自变量 ( x或 t ).

解的空间依赖性： X(x)

弦两端的边界条件为u（x，t）=0在弦的极端处坍缩至零。不幸的是，当K>0时，波动方程的通解产生了一个指数衰减和增长的总和，无法达到边界条件（除了通解u（x，t）=0）；因此K<0，这意味着我们必须引入复数，因为√K方程2.4.5中的术语。因此，我们可以重写K: 

和方程 2.4.4b 可以表示为

方程2.4.2形式的微分方程的通解是

用方程2.4.1导入得到

方程2.4.1中的复指数可通过欧拉公式表示为三角函数

合并同类项

方程2.4.4中的通解可以通过引入新的复数常数来表示为振荡函数 C=A+B和 D=i(A-B)

现在，我们应用方程2.4.5中的边界条件确定常数C和D。代入第一个边界条件(X(x=0)=0)代入方程2.4.5的通解，得到结果

并代入第二个边界条件(X(x=L)=0）代入方程2.4.5的通解得到结果

我们已经知道C=0从第一个边界条件得到方程2.4.8简化为

根据正弦的性质，公式2.4.8简化为

n=0时是忽略的无意义解，因此n=1,2,3... .

代入公式2.4.9以及2.4.7代入公式2.4.5得到结果

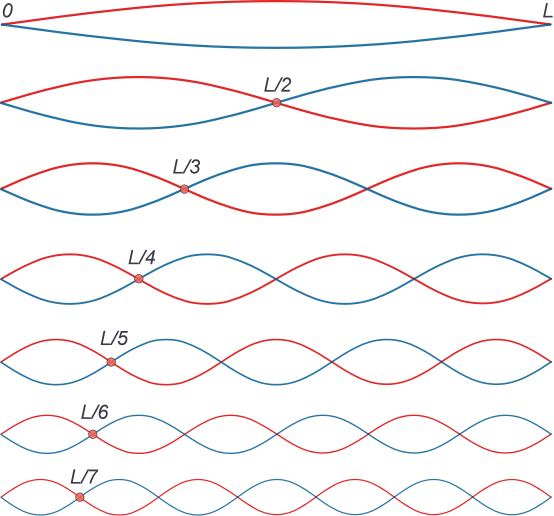
公式2.4.10给出了波方程在边界条件下空间部分解的一组解（图2.4.1)。这组解是无限大的，每个解都由n个不同的元素来区分参数引入以考虑边界条件。这个数字是“量子数”的一个例子，量子数在量子力学中普遍存在，并且对于每个系统都是唯一定义的。

图2.4.1：前7个X(x)长度为L的振动弦的解在最大位移的两个时刻（红色和蓝色）。

解的时间依赖性：T(t)

类似的论点也适用于假设的另一半(T(t))最初是为经典波动方程提出的，它是通过求解方程2.4.4a得到的，它定性地类似于上面求解的原始空间微分方程（方程2.4.4b)。

然而，从解决空间依赖性中提取的约束也适用于时间依赖性。当方程2.4.1以及2.4.9代入公式2.4.4a，得到一个更简化的表达式

定义一个新常量：ω_n

并代入方程 2.4.11

其与公式2.4.2的函数形式相同。

与空间依赖性解相比，我们没有边界条件来确定常数E和F.

叠加原理

现在让我们重新审视经典波动方程（方程2.4.1）的原始假设解。，可使用方程式2.4.10进行替换以及2.4.12 

引入n对每个E和F的依赖性，其中n可能是独立的

方程式2.4.13中表示的函数是一组包含空间和时间特征的解，可以解决两端被紧束缚的弦的波动方程。

波动方程的线性度

波动方程有一个非常重要的性质：如果我们有两个方程的解，那么两个的和也是方程的解。检查这一点很容易：

具有该性质的任何微分方程称为线性微分方程。另外注意，如果a和b是常数，af(x,t)+bg(x,t)这也是方程的解。所以你可以把波动方程的任意两个解的倍数相加——叠加——来找到一个满足该方程的新函数。

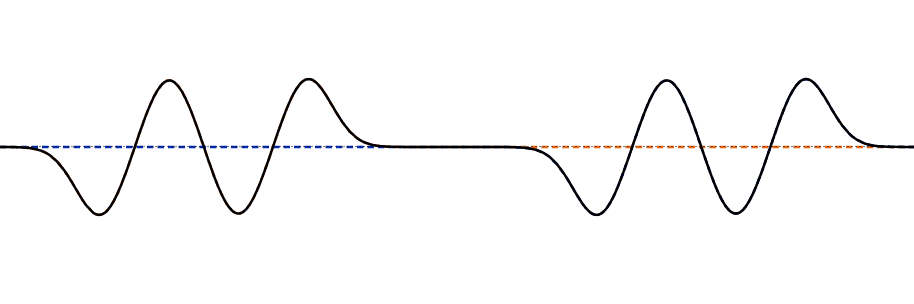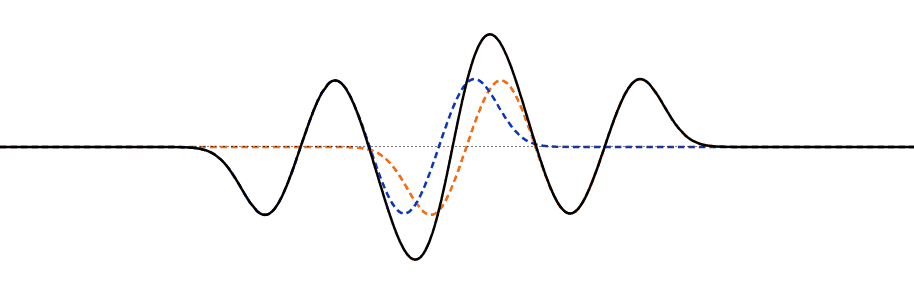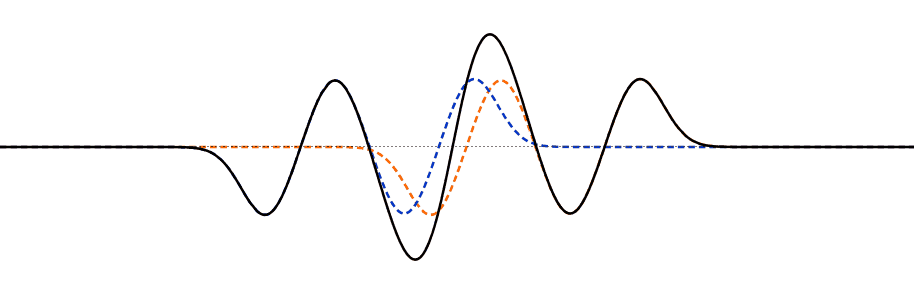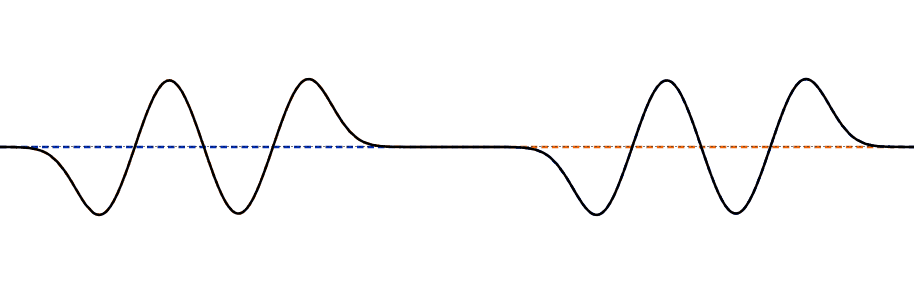
线性特性很容易从视觉上理解：如果可以画出两个波形解，那么在弦上的每一点上，只需将位移un(x,t)相加即可。从一个波到另一个波的um(x,t)，两波的叠加是一个解。例如，当两条沿弦向相反方向传播的行波相遇时，任意时刻任意点的弦位移就是这两条波各自单独作用时产生的位移之和。

这个简单的位移相加就是干涉，毫无疑问，因为如果相遇的波的位移方向相反，那么弦的位移就会比单个波小。这也就是所谓的叠加原理。

图2.4.2多脉冲干扰。

叠加原理

叠加原理是两个或多个解之和也是一个解。

由于波动方程是一个线性齐次微分方程，因此总解可以表示为由方程2.4.13描述的所有可能解之和。 .

每个un（x，t）该解称为系统的正常模式，可通过其对应的频率nπ/L来表征n=1、2、3...前七个正常模式的空间依赖性如图2.4.1所示是驻波。第一项n=1通常称为基频，而每个后续模式则称为泛音或谐波。正常模式的时间依赖性是正弦的，角频率为ωn可以扩展到自然频率νn经由

因此，当正常模式的空间曲率增加时，该模式的时间振荡也会增加。这是量子力学系统的一个共同特征，是波动方程的直接结果。