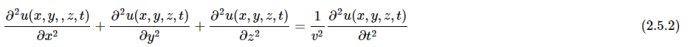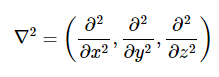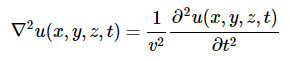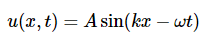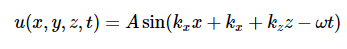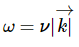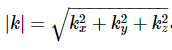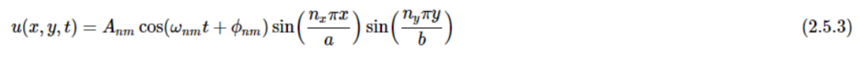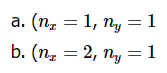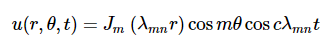2.5：振动膜

学习目标

l 将波动方程应用于二维膜（矩形和圆形）

l 认识二维系统中节点的可能几何形状

到目前为止，我们研究了一维波，沿着弦传播或沿狭窄管道传播的声波。然而，高维波也非常熟悉——池塘表面的水波，或者三维空间中从源头向外传播的声波。令人愉悦的是，这些高维波满足了波动方程，这是对我们找到的弦波动方程的一个非常自然的扩展，而且非常重要的是，它们还满足叠加原理，换句话说，如果波相遇，只需将每个波的贡献相加。在接下来的两段中，我们将更详细地讨论，但这一叠加原理是关键所在。

更高维度的波动方程和叠加

在更高维度中会发生什么？让我们考虑两个维度，例如鼓面等弹性片中的波。如果弹性片的静止位置是(x, y)平面，因此当它振动时，在z方向上上下移动，其在任意时刻的构型是一个函数u(x,y,t)

事实上，我们可以像处理弦一样，观察一小段上的总力并应用牛顿第二定律。在这种情况下，这意味着取鼓面的一小部分，而不是用拉力两端的细绳，而是用弹性片的一小块，张力沿着边缘拉伸。记住，这部分弦上的合力是因为弦弯曲而产生的，所以两端的张力方向略有不同，并没有相互抵消。∂²/∂x²测量曲率的参数是斜率的变化率。在二维情况下，想象弹性片的一小块，情况就更复杂了。将这块片子暂时想象成气球上的一个小区域，你会看到它在两个方向上弯曲，张力必须在边缘处拉扯。作用在这个小区域上的总力是因为表面弯曲时，相对两侧的张力方向不一致，现在我们必须加上来自两侧几乎相反的两组力。数学公式在这里展示，但至少可以推测方程为：

这个方程的物理原理是，薄片的一小部分的加速度来自于薄片在x方向和y方向弯曲引起的不平衡张力，这就是为什么左边有两个项。而且，进入三维空间很容易：再加一个项得到

这个空间上的部分微分之和在物理学中非常常见，有一个简写：

因此，公式2.5.2可以更简单地写为

正如我们在一维中发现的那样，传播谐波（无边界条件）

ω=νk时，可以验证三维方程有谐波解

其中

k→是波运动方向上的一个矢量。无线电波或光波中的电场和磁场具有这种形式（或者，更接近源的地方，对于向外传播的球面波，而不是平面波，有一个非常相似的等效表达式）。

重要的是要认识到二维波方程（方程2.5.1)仍然是一个线性方程，因此叠加原理仍然成立。如果两个波在弹性片或池塘表面相遇，任何一点的结果只需将各自波的位移相加即可。我们先从二维和三维中自由传播的波开始思考，然后再考虑受限区域内的波，比如鼓面。

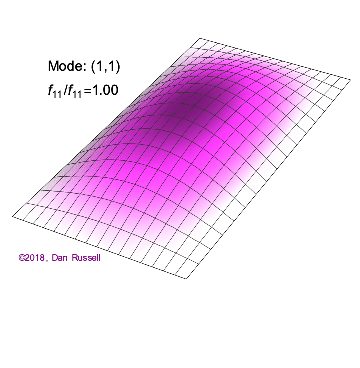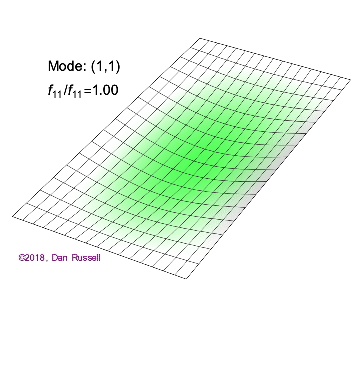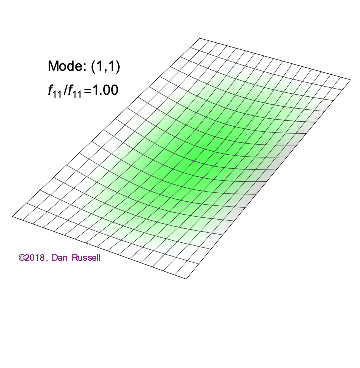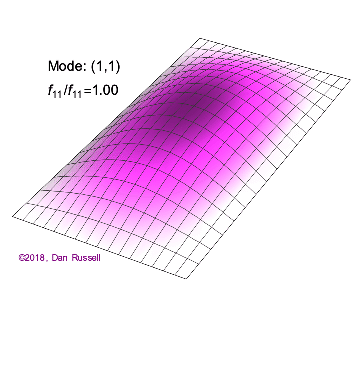
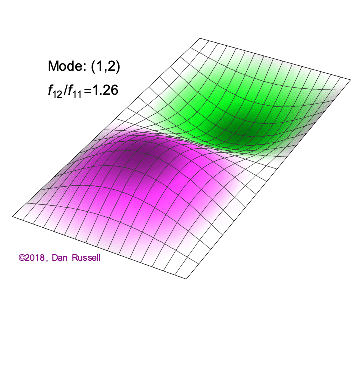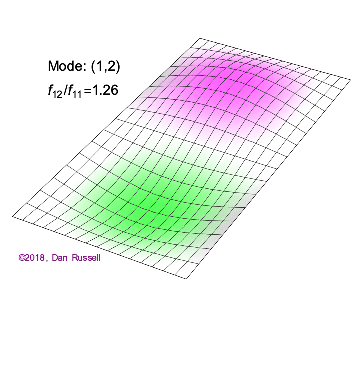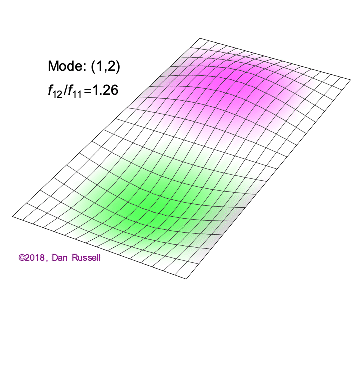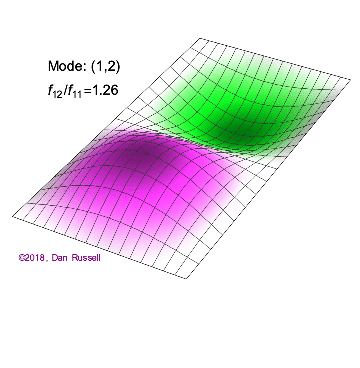
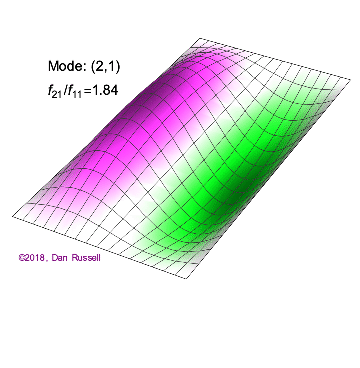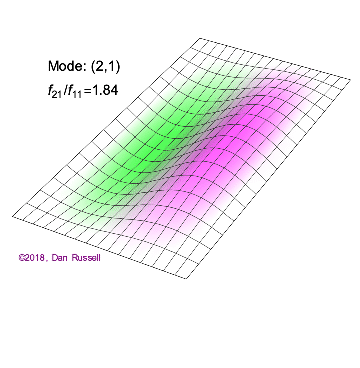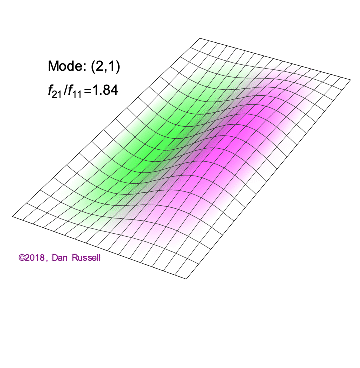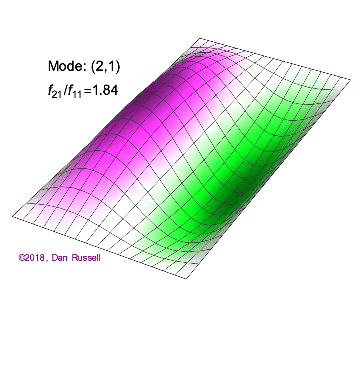
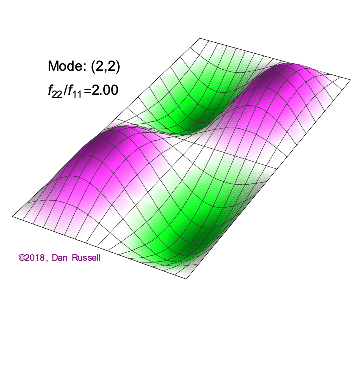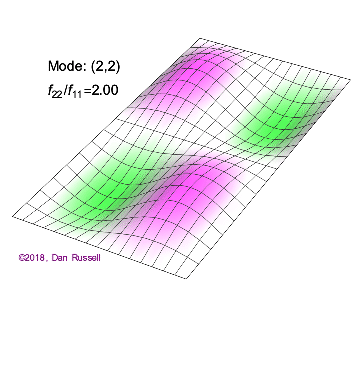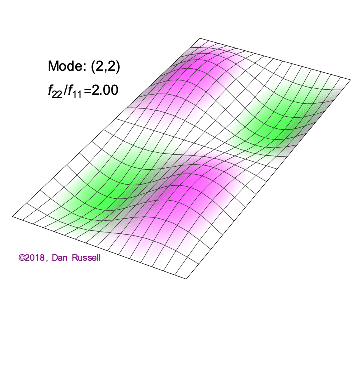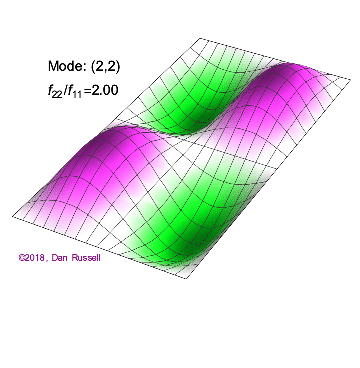
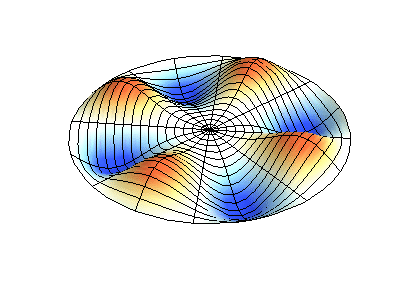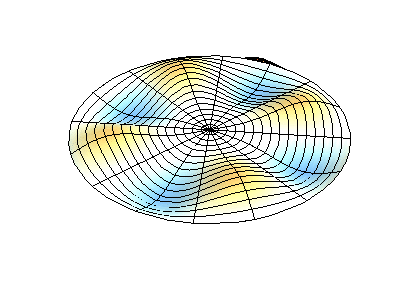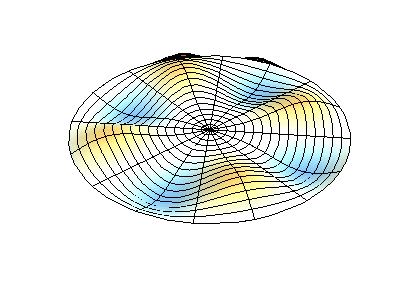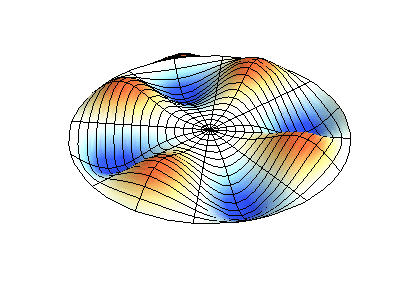
矩形膜的振动模式

一维波在传播方式上没有选择：它只是沿着直线移动（当然，由于线的变化，部分可能会被反射，一部分则会向后传播）。然而，当我们进入更高维度时，起始于某个局部区域的波动如何扩散就远非显而易见了。但我们可以先回顾一些简单的情况：向静水中投入一颗小石子，会在水面形成向外扩散的圆形涟漪。如果我们承认光是一种波，我们会注意到光束从空气进入玻璃时方向会发生变化。当然，光是波这一点并非立即显而易见：我们稍后会详细讨论这一点。下面展示了几个解（包括时间和空间上的），以及它们的量子数(nx和ny）。

(nx=1, ny=1)的解

(nx=1, ny=2)的解

(nx=2, ny=1)的解

(nx=1, ny=2)的解

图2.5.1：选择矩形膜的振动模式。

求解函数u(x,y,t)在振动的矩形膜中，通过变量分离和设定边界条件来求解。求解出的函数非常相似，其中

这里

l a是矩形膜的长度和b是宽度，

l nx和和ny是两个量子数（每个维度一个）

与一维波方程的解一样，节点是结构上不移动而其余部分振动的点（或线）。

例 2.5.1：矩形膜中的节点几何形状

对于图2.5.1中的以下二维解，有多少节点，几何形状是什么，你如何描述它们？

解决方案 a

(nx=1,ny=1)图2.5.1中的解没有节点。也就是说，在膜的运动过程中，膜上没有任何位置（边界除外）是静止不动的。

解决方案 b

(nx=2,ny=1)图2.5.1中的解决方案有一个节点。它是一条线，长度为x方向的一半，并延伸至y方向的整个长度。

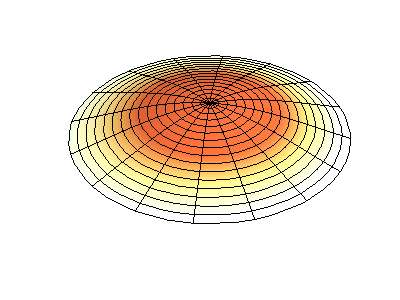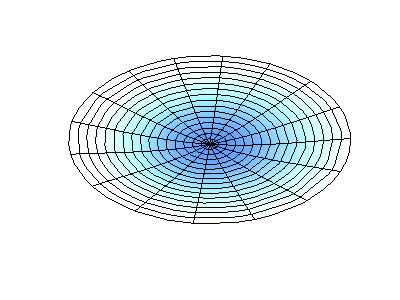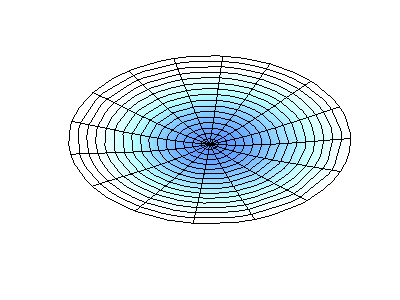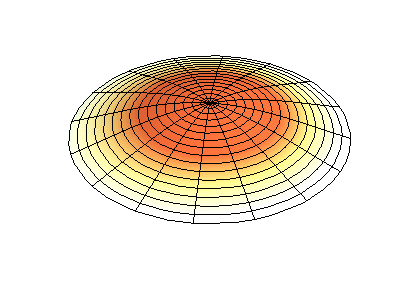
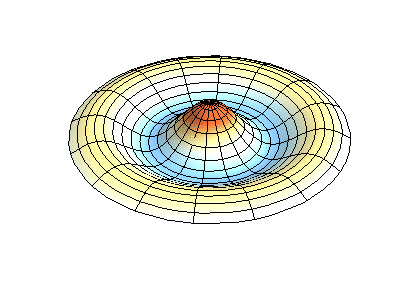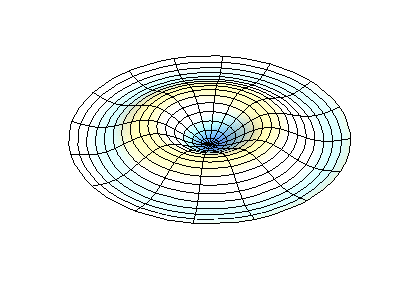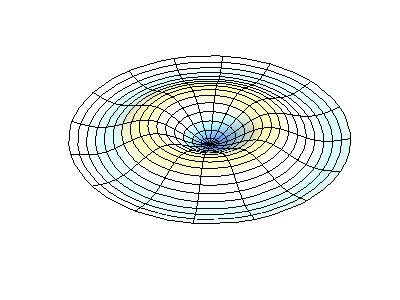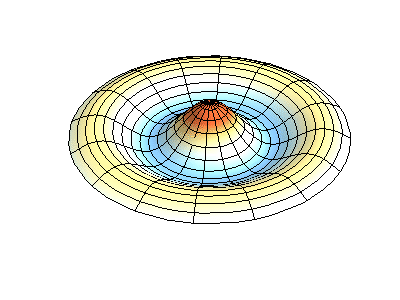
圆膜的振动模式

振动矩形膜的基本原理适用于其他二维构件，包括圆形膜。但是，数学和解法稍微复杂一些。最好用极坐标表示解法（而不是像方程2.5.3那样的矩形）。并且具有以下函数形式

其中Jm是贝塞尔函数（这些是振荡函数）和λ是常数。这个系统有两个量子数(m和n)，其函数形式与在矩形膜中的nx与ny相同。在图2.5.2的动画中，节点直径和圆圈显示为不振荡的白色区域，而红色和蓝色区域表示正负位移。

图2.5.2选择圆形膜的振动模式。

图2.5.2（左）显示了振动圆形膜的基本模式形状，而其他两种模式是具有更复杂节点特性的激发模式。