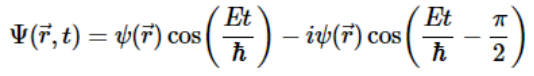3.1：薛定谔方程

学习目标

介绍薛定谔方程的一般性质及其解。

德布罗意的博士论文于 1924 年底答辩，在欧洲物理学界引起了不小的轰动。1925 年秋天，苏黎世理论物理学教授、爱因斯坦的继任者彼得·德拜 （Pieter Debye） 向埃尔温·薛定谔 （Erwin Schrödinger） 建议他就德布罗意的工作举办一次研讨会。薛定谔作了一个优美的演讲，但在最后，德拜说他认为整个理论相当幼稚：为什么波应该将自己局限在太空中的一个圆圈中？这个圆圈并不是一个挥动的圆绳，太空中的真实波会衍射和扩散，事实上，它们服从三维波动方程，这就是所需要的。这对薛定谔来说是一个直接的挑战，他花了几周时间在瑞士山区研究这个问题并构建他的方程。薛定谔方程没有从先前建立的理论中严格推导出来，但通过考虑光波和光子之间的联系，并为德布罗意的波和电子（以及后来的其他粒子）构建一个类似的结构，可以使其变得非常合理。

薛定谔方程：更好的方法

虽然玻尔模型能够预测任何单电子原子或阳离子的允许能量，但它绝不是一种普遍的方法。此外，它严重依赖于经典思想，笨拙地将量子化嫁接到本质上是经典的图景上，因此无法真正揭示原子的真实量子性质。任何可能预测量子系统允许能量的规则，都必须考虑波粒二象性，并隐含地包含粒子的波动描述。尽管如此，我们将尝试一个启发式论证，使结果至少显得合理。在经典电磁理论中，根据麦克斯韦方程组可以推导出真空中的电场和磁场的每个分量都是三维波动方程的解：

方程3.1.1中的波动方程是前面提出的波动方程（方程2.1.1)的三维模拟，其中速度固定为已知的光速：c。而不是偏导数∂²/∂x²在某一维度中，引入拉普拉斯（或“del平方”）算子：

相应地，这个三维方程波方程的解是四个独立变量的函数：x,y,z,和t通常称为波函数ψ.

现在我们将尝试为德布罗意的物质波创建一个类似的方程。因此，让我们考虑仅在一维空间中沿x方向传播的波动。在某一时刻，波动的形式可以用如下函数表示：

其中f(θ)表示正弦函数，例如sinθ, cosθ, e^iθ,  e^−iθ或者是这些函数的线性组合。最具有启发性的形式是复指数函数，它与正弦和余弦函数通过欧拉公式有关。

以上每个函数都是周期函数，每当其参数增加2π时，x将增加一个波长λ。在空间的固定点上，波的时间依赖性具有类似的结构：

其中ν给出波的周期数与单位时间的关系。同时考虑x和t在依赖性中，我们考虑形式为的波函数

表示从左向右传播的波。现在我们利用普朗克公式(E=hν)和德布罗意公式(p=h/λ)由它们的粒子类比以替换ν以及λ。这给出了

这里

由于普朗克常数出现在大多数公式中，分母为2π，ℏ符号由Paul Dirac引入。公式3.1.5在某种程度上代表了具有能量E的粒子的波形性质动量p。方程3.1.7的时间导数得到

因此，从方程3.1.7以及3.1.9的简单比较中可以看出

或类似地，方程3.1.9关于x微分

然后是二阶导数

非相对论性自由粒子（即所有能量都是动能，不涉及势能）的能量和动量关系如下

代入方程3.1.12以及3.1.10代入公式3.1.13显示Ψ（x,t）满足以下偏微分方程

公式3.1.14是描述自由粒子波函数的适用微分方程，该粒子不受任何外力约束，或者等效地不在其势能V(x,t)为零的区域。

对于具有非零势能V(x)的粒子，总能量E则为动能和势能之和

我们假设方程3.1.3因为物质波可以推广到

对于三维中的物质波，方程3.1.6然后展开

这里为势能和波函数Ψ取决于三个空间坐标x,y,z，为了简洁起见，我们将其写为r→注意，假设势能仅依赖于位置而与时间无关（即粒子运动）。这适用于保守力，其势能函数为V(r)可以得到。

这拉普拉斯算子

括号里的三个二阶导数统称为拉普拉斯算子，或del平方，

使用 del 运算符

请记住，当del算子直接作用于一个场（例如，∇f（x，y，x）时，表示场的梯度（即局部最陡斜率）。方程3.1.19中的带箭头符号是单位向量。

公式3.1.17是描述波函数振幅Ψ(r,t)的时间依赖薛定谔方程与粒子在指定势场V(r)内的物质波相关。1926年，海森堡提出了矩阵力学（1925年，海森堡提出了另一种版本的量子力学）。

对于保守系统，能量是一个常数，时间依赖因子来自方程3.1.7可与空间因素分离（通过第2.2节中讨论的变量分离技术）

其中ψ(r→)是波函数依赖（或时间独立）的波函数，仅依赖于空间坐标。将方程3.1.20代入公式3.1.17取消指数因子，我们得到时间无关的薛定谔方程：

方程3.1.21的总体形式这并不罕见或出乎意料，因为它运用了能量守恒原理。我们大多数将量子力学应用于化学的情况都将基于这个方程（光谱学除外）。时间独立薛定谔方程的各项可以解释为系统的总能量，等于系统动能加上系统势能。在这方面，它与经典物理学完全相同。

Wavefunctions 的时间依赖性

请注意，与时间独立的薛定谔方程一起使用的波函数（即ψ(r→))没有明确的t依赖关系，如方程3.1.17中时间依赖类的波函数(i.e.,Ψ(r→,t))。这并不意味着波函数没有时间依赖性。方程3.1.20认为时间依赖的（即，完整的空间和时间）波函数(Ψ(r,t))，与时间无关（即，仅空间）波函数ψ(r→)不同由“相位因子”引起，其大小为常数。使用方程3.1.4中的欧拉关系式，上述总波函数可以展开

这意味着总波函数具有复数特性，包含实部和虚部。此外，利用三角恒等式sin(θ)=cos（θ−π/2），公式3.1.22可进一步简化为

这表明总波函数的实部和虚部都振荡，总波函数的虚部对于实部相位相差π/2。请注意，虽然所有波函数都具有时间依赖性，但这种依赖性可能不会影响简单的量子问题，如下几节所讨论的，通常可以忽略不计。

然而，在我们开始之前，让我们暂停一下，评论量子力学的有效性。尽管它显得怪异、抽象，且将宇宙视为一个充满随机性和不可预测性的场所，量子理论仍经受了严格的实验检验。结果发现，它的预测与实验相符的程度优于10⁻¹⁰%。对于迄今为止研究的所有案例。当薛定谔方程与电磁场的量子描述相结合时，形成了一种被称为量子电动力学的理论，这是迄今为止提出的最精确的物质理论之一。牢记这一点，让我们继续讨论量子宇宙以及如何将量子理论应用于模型和实际情境中。