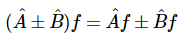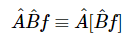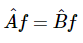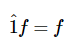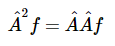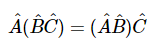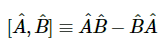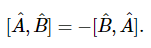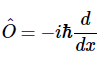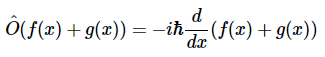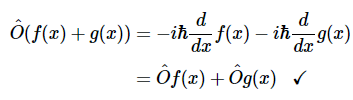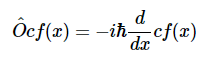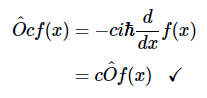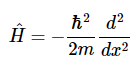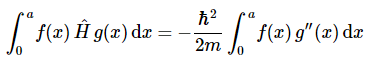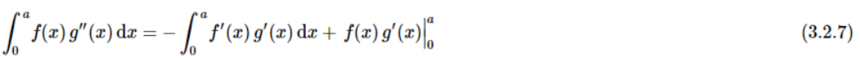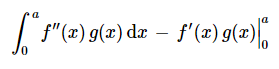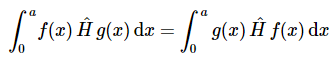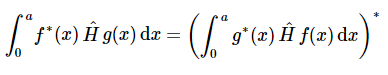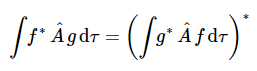3.2： 量子力学中的线性算子

学习目标

在量子力学中，经典力学量由线性算子表示。

理解标量和函数的“代数”运算并不总是等同于算子（特别是交换律）。

时间独立薛定谔方程（一维）中的括号内对象

被称为算子。算子是对函数概念的推广，即应用于另一个函数。函数是将一个数转换成另一个数的规则，而算子则是将一个函数转换成另一个函数的规则。对于时间独立的薛定谔方程，相关的算子是哈密顿算子（通常简称为哈密顿），这是量子力学中最常见的算子。

我们通常（但并非总是）通过在对象上加一个“帽子”来表示它是一个运算符，例如，H^因此，时间独立的薛定谔方程可以从方程3.2.1中简化。

方程式3.2.2哈密顿算子作用于波函数，产生能量，即能量是波函数的标量（即一个数值、量和可观测量）乘以波函数。这种方程，其中算子作用于函数，产生一个常数乘以该函数，被称为特征值方程。这里的函数称为特征函数，产生的数值称为特征值。‘Eigen’在德语中意为‘自我’或‘自身’。我们将在后续章节中详细讨论这一点。

运算符的基本属性

运算符的大多数属性都很简单，但为了完整起见，下面总结了它们。

两个算子A^的和与差以及B^由下面公式给出

两个运算符的乘积定义为

如果两个运算符相等，则

标识运算符1^什么都不做（或乘以1）

第n运算符A^n定义为n运算符的连续应用，例如。

运算符的结合律成立

交换律通常不适用于运算符。一般来说，但并非总是如此，

帮助确定方程3.2.3中的不等式是否成立，对于任意两个特定的算子，我们定义对易算符。

定义：对易算符

定义对易算符A^和B^对易是简单的

如果对易不为零，则作顺序很重要，运算符称为 “非对易”。此外，此属性适用

线性运算符

将函数f(x)集成到函数中g(x)表示为

最常见的运算符类型是线性运算符，它满足以下两个条件：

和

l O^是一个线性算子，

l c是一个常数，可以是复数形式(c=a+ib)和

l f(x)以及g(x)是关于x的函数

如果运算符无法满足任一方程3.2.5或3.2.6，那么它就不是线性运算符。

例 3.2.1

这个运算符是否为线性？

解答：

要确认操作员是否为线性，需满足方程3.2.6中的两个条件必须予以证明。

条件A(方程3.2.5):

从基础微积分学中，我们知道可以使用求和法则进行微分。

条件A已确认。条件B(方程3.2.6)合理吗？

同样，根据基本微积分原理，这个也可以从导数中分离出来

是的。此运算符是线性运算符（这是线性动量运算符）。

在量子力学中遇到的大多数运算符是线性运算符。

厄米算符

通过考虑粒子在盒内的哈密顿量，可以发现算子的一个重要性质：

设f(x)以及g(x)是满足与H^的特征函数相同的边界条件的任意函数。例如，它们在x=0处消失并且x=a。考虑积分

现在用偏微分

根据对f以及g的假设条件，边界项消失。通过部分积分法对方程3.2.7进行第二次积分。得到

因此，

复函数的明显推广形式如下

在数学术语中，运算符A^是为了

对于所有函数f以及g遵循特定边界条件的算子被归类为厄米特或自伴算子。显然，哈密顿算子是一个厄米特算子。假设所有表示动态变量的量子力学算子都是厄米特的。该术语也用于线性代数课程中矩阵的具体时间点。

所有表示动态变量的量子力学算子都是Hermitian算子。