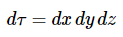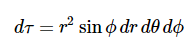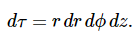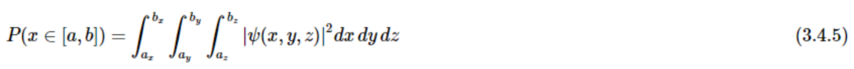3.4：波函数具有概率的解释

学习目标

理解波函数可以有概率解释。

直接从波函数计算概率

对于单粒子系统，波函数Ψ（r，t），或ψ(r)对于时间独立的情况，它表示尚未明确界定的物质波的振幅。由于波函数通常为复数函数，因此无法仅从函数本身推导出其物理意义，因为√−1这不是物理世界的一个属性。相反，物理意义在于波函数与其复共轭的乘积，即波函数的绝对值平方（也称为模的平方，或绝对值）。

其中r是一个向量（x，y，z）在三维空间中指定一个点。这里使用的是平方，而不是模数本身，就像光波的强度取决于电场的平方一样。

波函数的平方（方程3.4.2）在1926年被提出，这是最广泛接受的波函数解释。与电子在位于半径为ri的体积内dτ的概率密度（即单位体积内的概率）成正比。由于波函数体现了物质的波动特性，因此概率振幅P（x，t）还将表现出波动性。概率密度是双缝衍射实验中电子在二维屏幕上出现的衍射图案的三维对应物。认为我们只能通过概率来理解原子和分子世界的想法，让一些人感到不安，他们希望通过持续的研究寻找更令人满意的描述。

根据波恩的解释，波函数被称为概率振幅，其绝对值平方则称为概率密度。此外，将概率密度乘以三维空间中的体积元素(dτ)是概率P

如果对其位置进行测量的话在空间维度中移动的单个量子粒子出现在区域x∈[a，b]内的概率

三维情况下，方程3.4.3表示方式不同

这种集成覆盖了指定的体积(V)，用符号dτ表示指定所采用坐标系的适当体积元素（包括雅可比矩阵）：

笛卡尔空间：

球空间：

圆柱空间：

对于直线笛卡尔空间，方程3.4.4可以扩展并明确指示维度

积分的上下限被选定以包含体积V值得考虑。

波恩解释方程3.4.2将波函数与概率联系起来，对波函数的数学行为提出了某些要求，任何数学函数都不能成为有效的波函数。

Wavefunction 的必需属性

l 波函数必须是所有坐标的一个单值函数，因为概率密度应该在空间的每个点上唯一确定。

l 波函数应该是有限的，因为无限的概率是没有意义的。

l 波函数应该在任何地方都是连续的，正如一个物理上有意义的概率密度所期望的那样。

波函数必须是单值的、有限的且连续的——简而言之，即“行为良好”——这些条件对薛定谔方程的解施加了限制，使得只有特定的能量值和其他动力学变量被允许。这一过程被称为量子化，是量子力学命名的关键特征。

需要注意的是，这种解释表明波函数并不意味着粒子像“电荷云”那样分布在大范围内。波函数用来描述电子的运动，这种运动表现出波动性，并满足波动方程。这类似于在大型班级中，成绩分布并不代表某个学生的成绩被模糊化，而是在考虑成绩分布是基于多个可测量因素（如学生的表现）的结果时才有意义。