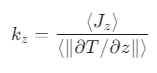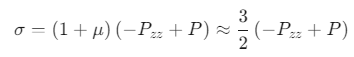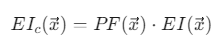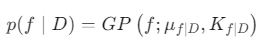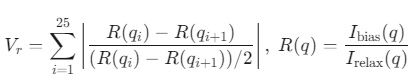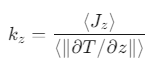*欢迎大家去观看原文，并引用

标题：Inverse Design of Block Polymer Materials with Desired NanoscaleStructure and Macroscale Properties

期刊：JACS Au

网址：https://doi.org/10.1021/jacsau.5c00377

一、文章摘要

由于聚合物的设计变量数量众多，因此设计具有特定材料特性的新型聚合物一直是一个长期存在的挑战。为了加快这一设计过程，迫切需要开发新的工具来辅助逆向设计过程，并有效地探索高维聚合物设计空间。对于聚合物体系而言，优化宏观材料特性比无机物和小分子更具挑战性，因为这些特性受多种长度尺度上的特征所决定，从选定的单体化学结构到链级设计，再到更大的尺度（纳米至微米）的结构域结构。在这项工作中，我们提出了一种高效的高通量基于计算机模拟的框架，以有效地设计具有所需多尺度纳米结构和宏观特性（我们称之为 RAPSIDY2.0 -聚合物结构快速分析和逆向设计策略2.0）的高性能聚合物（共混物、共聚物）。RAPSIDY 的新版本基于我们之前的 RAPSIDY1.0工作，后者仅专注于确定能够稳定所需纳米级形态的聚合物设计。在 RAPSIDY2.0 中，我们采用了分子动力学（MD）模拟与基于贝叶斯优化的主动学习相结合的方法，以最优方式查询高维聚合物设计空间，并提出具有潜力的设计候选方案，这些方案既能稳定选定的纳米级形态，又能展现出所需的宏观级材料特性（例如拉伸强度、热导率）。我们利用已将聚合物链预先置于选定纳米级形态中的 MD模拟，并进行虚拟实验以确定所选聚合物设计在目标形态内的稳定性，并计算所需的宏观级材料特性。我们的方法直接解决了共聚物所特有的挑战，因为其宏观级特性取决于链设计和介观形态，而这两者是相互关联的。

二、计算图文

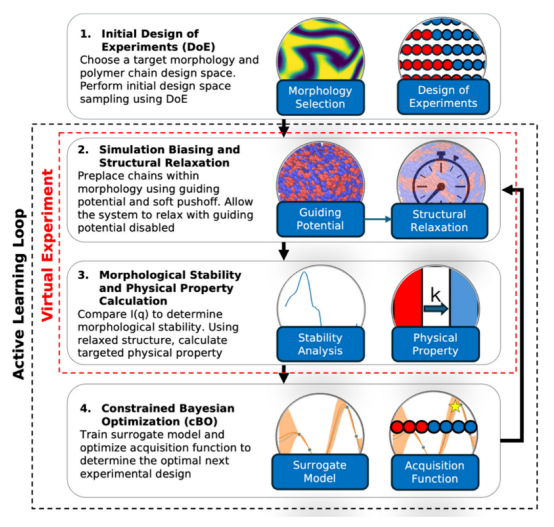
图 1.RAPSIDY2.0框架概述。我们的方法首先确定目标形态，并通过数学方式定义目标聚合物设计空间。我们使用标准的设计实验（DoE）技术（如拉丁超立方体采样（LHS）、全因子设计和完全随机设计）进行初始采样。在这里，我们使用 LHS，因为它具有近乎随机的设计以及高效的超体积填充能力。使用选定的设计参数，我们进行计算机模拟实验（仿真）以确定形态稳定性和目标物理性能。我们利用之前的 RAPSIDY1.0 方法，并使用引导势能将链置于目标形态中，然后让系统在引导势能的作用下松弛，以确定链设计与形态之间的兼容性。与 RAPSIDY1.0 不同，我们不再并行筛选多个晶格常数（盒子大小），而是让主动学习循环来确定最佳的盒子大小。最后，我们采用约束型贝叶斯优化方法来确定接下来要测试的最优设计方案，具体做法是训练成本较低的替代模型来预测形态稳定性以及目标物理特性，并优化获取函数以确定进行虚拟实验的最优设计方案，从而实现闭环控制。

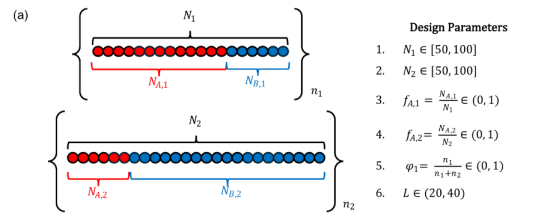
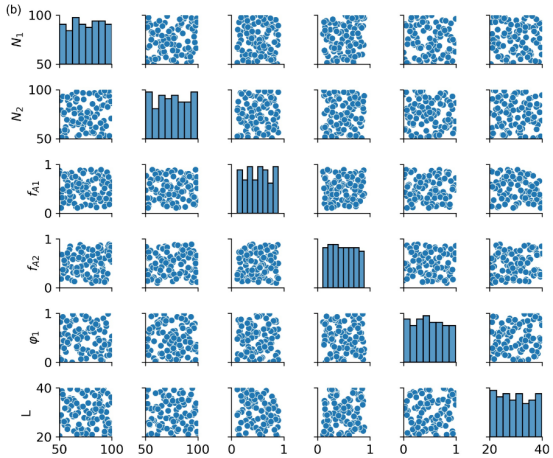
图 2.利用拉丁超立方抽样对二嵌段共聚物混合物的设计空间及初始设计实验（DoE）进行设计。（a）二嵌段共聚物混合物的设计空间为6维，其中包含五个与链结构和混合设计参数相关的参数，包括链长、A 的体积分数和混合比例，还有一个与模拟盒尺寸相关的参数。引入模拟盒尺寸参数对于二嵌段共聚物的计算机模拟实验而言是独特的，旨在解决标准二嵌段共聚物模拟中众所周知的“盒尺寸不协调”问题，如文中所述。（b）使用拉丁超立方抽样进行实验设计采样的两两关系，共100 个样本。对角图显示单变量分布，非对角图显示两两相关性。

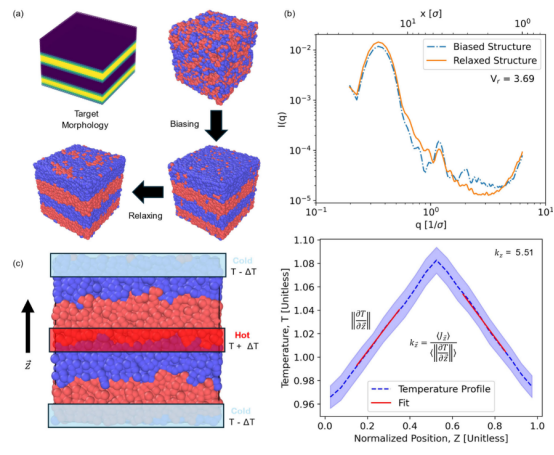
图 3.示意图展示了利用示例层状目标结构计算热导率的虚拟实验步骤。（a）与 RAPSIDY1.0 中的做法相同，将随机无序的熔体引导形成目标形态（在本图中为层状相）。在实现目标形态后，禁用引导势能，让系统自然地松弛至其局部能量最低点。（b）使用偏置结构和松弛结构的波动率比 Vr相似性（即偏置结构和松弛结构的散射曲线之间的相似性）来量化目标形态与所选链设计的兼容性。Vr值越低，稳定性越高。（c）使用非平衡分子动力学进行热导率计算。使用直线曲线拟合温度分布，以确定平均温度梯度和热导率值 kz。

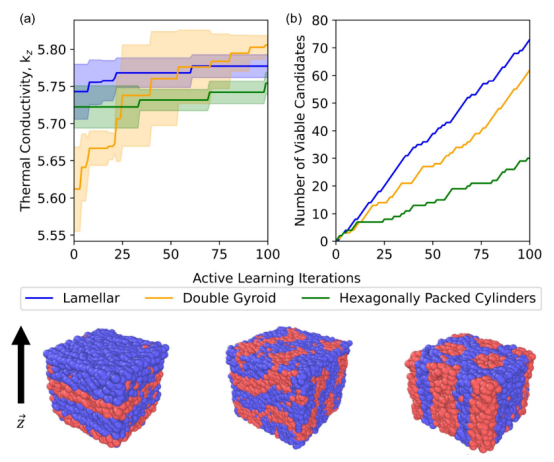
图4. 不同目标形态下热导率的约束式贝叶斯优化结果。（a）经过100 次主动学习迭代后，层状、双网格状和六边形排列圆柱体的前10个候选物的平均热导率及标准偏差。（b）使用 cBO找到的满足 Vr阈值的可行候选物的数量，该数量随主动学习迭代次数的变化而变化。cBO有效地将搜索范围限制在具有目标形态的设计参数范围内。

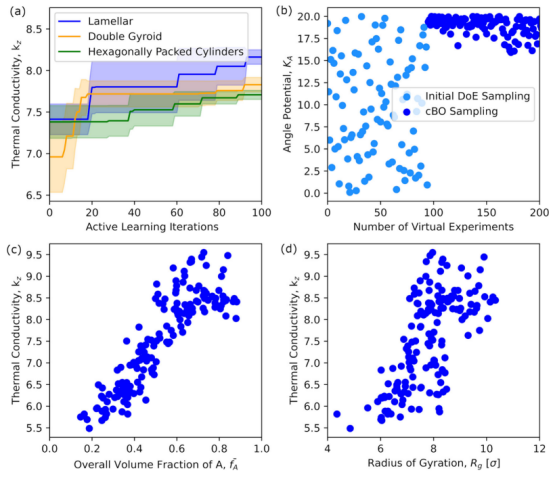
图5. 不同目标形态（A块灵活性各异）的约束型贝叶斯优化结果。（a）经过100 次主动学习迭代后，层状、双螺型和六边形排列圆柱体的前10个候选物的平均热导率及标准偏差。（b）对于层状目标形态，采样角度势值在初始设计空间内的值（浅蓝色）和在主动学习期间的值（蓝色）。主动学习旨在通过最大化链的刚度来最大化热导率。（c）在主动学习期间，层状目标形态下热导率与 A 的总体体积分数之间的关系。使系统内硬块总体积最大的样本会得到更高的热导率值。（d）在主动学习期间，对于层状目标形态，整个共聚物链的规整半径之间的热导率与之的关系。

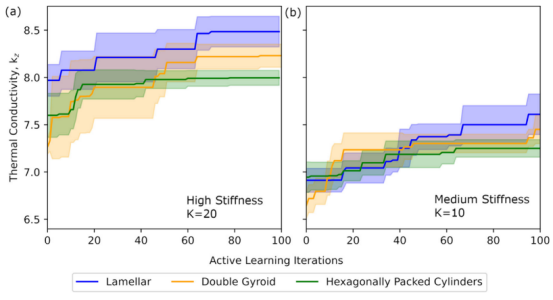
图 6.针对不同目标形态且固定刚度的情况，进行约束式贝叶斯优化的结果。（a）高刚度情况，K =20；（b）中等刚度情况，K =10。有关刚度较低（K =0）的柔性链，请参考图4。

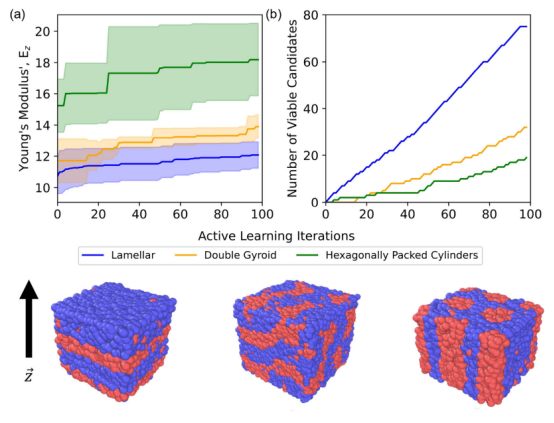
图 7.不同目标形态下杨氏模量的约束贝叶斯优化结果。（a）经过100 次主动学习迭代后，层状、双柱状准晶和六边形排列圆柱体这三种形态的前10个候选物的平均杨氏模量及标准差。（b）使用 cBO找到的满足 Vr阈值的可行候选物的数量，该数量随主动学习迭代次数的变化而变化。cBO有效地将搜索范围限制在能够形成目标形态的设计参数范围内。

三、计算分析

3.1逆向设计方法学

约束贝叶斯优化（cBO）框架

通过数学推导将形态稳定性约束（Vr<4.5）整合至贝叶斯优化过程（公式9-12）：

EIc(x)=PF(x)⋅EI(x)

其中 PF(x)为满足形态约束的概率，EI(x)为标准预期改进函数（公式4-7）

设计空间高效搜索：cBO通过高斯过程代理模型（公式10）和采集函数优化，在7维参数空间（链长、体积分数、刚度等）中定位高性能材料。

分子动力学虚拟实验

形态稳定性验证：

施加外部引导势（公式3）将无序熔体预置为目标形态（层状/双连续Gyroid/柱状）

弛豫后通过散射剖面相似性 Vr（公式未编号）量化稳定性（Vr<4.5为稳定）

物性计算协议：

热导率：非平衡MD（NEMD）速度交换法（Müller-Plathe方法），拟合温度梯度得：

杨氏模量：单轴拉伸模拟（体积恒定），通过应力-应变曲线线性区拟合：

四、计算方法

4.1核心计算方法

1. 约束贝叶斯优化（cBO）

数学框架

目标函数：maxc(x)≤λf(x)

（f(x)=目标物性，c(x)=形态稳定性约束，λ=约束阈值）

约束改进函数：

EIc(x)=PF(x)⋅EI(x)

PF(x)= 满足Vr<4.5的概率

EI(x)= 标准预期改进函数（公式4-7）

代理模型：高斯过程（GP）先验

使用Matern协方差核建模

2. 分子动力学虚拟实验

形态稳定性验证

引导势：

（A=100，φ^ref=目标形态密度场）

稳定性判据：散射剖面相似性Vr（Vr<4.5为稳定）

物性计算

热导率（NEMD法）：

速度交换频率：每10步，总时长106τ

杨氏模量（单轴拉伸）：

应变率：0.000001τ−1（总应变10%）

应力计算：σ≈23(−Pzz+P)

弹性区智能识别：滑动窗口t检验（p<0.05阈值）

4.2关键参数体系

1. 设计空间参数（7维）

注：设计空间采样采用拉丁超立方抽样（LHS），初始100个样本

2. 力场参数

非键作用：截断LJ势（r_cut=2σ）

εAA=εBB=1kBT, εAB=0.8kBT (χ=1.2)

键合作用：

键伸缩：U_bond(r)=50k_BT/σ²(r−r₀)² (r₀=σ)

键角弯曲（仅A嵌段）：U_angle(θ)=K[1+cos(θ)]

密度：ρ=0.45σ⁻³（熔体条件）

3. 模拟参数

4.3特殊计算技术

晶格常数参数化

将盒尺寸L作为优化变量，替代传统网格搜索，解决嵌段共聚物盒尺寸不相容问题

结构序参量分析

链取向度：S₂=3/2<cos²θ>−1/2

（θ=键向量与z轴夹角）

示例：层状相S2=0.25> 双连续GyroidS₂=0.16

代码实现：

RAPSIDY 2.0 GitHub