|
牛顿方程的数值解法和周期性边界条件时间:2025-05-06 设一个对象或系统由n个原子构成,这n个原子的位置为
对于有n个原子的系统就有n个运动方程。在每一时刻对这些方程进行积分并结合初始时刻所有原子的位置和速度就可获得后续任意时刻的原子位置和速度。系统所有原子任意时刻的位置和速度称为系统原子的轨迹。基于对系统原子轨迹的分析即可获得系统的性质和属性。给出了最原始的原子运动控制方程,该方程对应统计力学中的微正则系综。 对控制方程采用速度-Verlet法,该方法在不同的时间步计算原子的位置和速度,即在
由将上式重新改写为
上式中为
如果不需要
由于在实际的分子动力学模拟中,会先给定初始时刻系统内所有原子的位置和速度以及为避免在不同时间步计算位置和速度,通常采用如下更为简便的方法实施跳蛙法
周期性边界条件等价于在模拟区域周围放置与模拟区域完全相同的镜像。下图为二维情形下模拟区域及其周围的周期性镜像。周期性边界条件具有两个特点。第一个特点是当某个原子跨越一个边界时会立刻从对面的边界重新进入模拟区域。第二个特点与计算原子所受非键结力有关。我们知道原子间的非键结力在两个原子距离较远时可以忽略不计,因此在计算某个原子所受非键结力时,会设置一个截断半径
二维周期性边界条件示意图。 在计算原子位置以及原子受力时,周期性边界条件的这两个特点在每一步计算时都要被考虑。在每一步更新原子位置后,都要对原子位置与边界位置进行比较,如果超出边界位置,则需要替换掉直接计算得到的原子位置,使其重新回到模拟区域中。以 感谢鲍路瑶老师的分享,内容来自于鲍老师分享出来的资料 如有需要添加微信:lmp_zhushou 进入微信群,帮助他人,共建社区 获取完整版lammps讲义可以加微信lmp_zhushou或加入QQ群994359511 上一篇LAMMPS软件的并行通信算法下一篇温度、压强 |


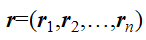 ,速度为
,速度为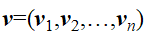 以及质量为
以及质量为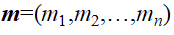 。原子受到的力为其总势能的梯度,由此根据牛顿第二定律建立任一原子的运动方程为
。原子受到的力为其总势能的梯度,由此根据牛顿第二定律建立任一原子的运动方程为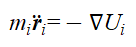
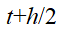 时刻更新原子的速度,然后在
时刻更新原子的速度,然后在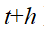 更新原子位置,最后再更新在
更新原子位置,最后再更新在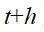 的速度。首先将
的速度。首先将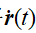 在
在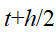 和
和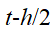 时刻进行泰勒展开,有
时刻进行泰勒展开,有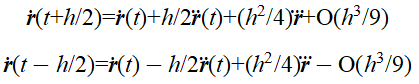
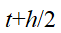 速度
速度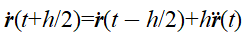
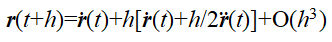
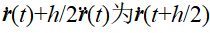 ,有
,有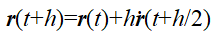
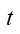 时刻的速度,则模拟过程中仅需存储
时刻的速度,则模拟过程中仅需存储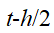 时刻的速度和
时刻的速度和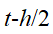 的速度获得
的速度获得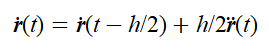
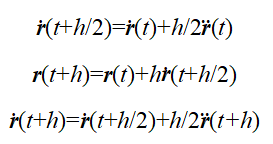
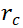 ,即一个原子只有处于以该原子为中心,
,即一个原子只有处于以该原子为中心,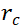 为半径的圆形区域(三维条件下为球形区域)内时才考虑这个原子对该原子的受力。周期性边界条件要求在计算边界附近原子的受力时,不仅要考虑本身模拟区域中截断半径以内的原子,还要将最近的周期性镜像区域中处于截断半径所表征区域内的原子也考虑在内,这就等价于考虑了在对面边界附近的原子。
为半径的圆形区域(三维条件下为球形区域)内时才考虑这个原子对该原子的受力。周期性边界条件要求在计算边界附近原子的受力时,不仅要考虑本身模拟区域中截断半径以内的原子,还要将最近的周期性镜像区域中处于截断半径所表征区域内的原子也考虑在内,这就等价于考虑了在对面边界附近的原子。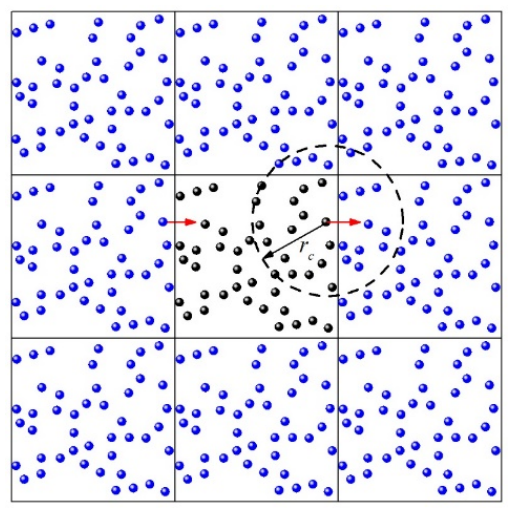
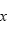 方向为例,设第
方向为例,设第 个原子的位置为
个原子的位置为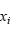 ,模拟盒子在
,模拟盒子在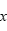 方向上的左右边界为0和
方向上的左右边界为0和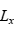 。每一时间步对
。每一时间步对 原子方向上的位置检测为:如果
原子方向上的位置检测为:如果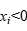 ,那么
,那么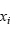 的值用替换
的值用替换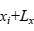 ;如果
;如果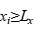 ;那么
;那么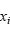 的值用替换
的值用替换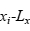 。在计算受力时,周期性边界条件具有类似的影响。考虑计算
。在计算受力时,周期性边界条件具有类似的影响。考虑计算 原子对
原子对 原子在
原子在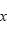 方向上的受力。设
方向上的受力。设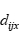 为两个原子在
为两个原子在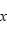 方向上的距离,如果
方向上的距离,如果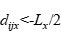 ,那么
,那么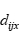 就用替换
就用替换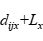 ;如果
;如果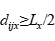 ,那么就用
,那么就用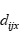 替换
替换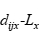 。由周期性边界条件的这两个特点可知,非键结力的截断半径的大小不能超过模拟区域最小尺寸一半。此外,在实际分子动力学模拟中,当某个原子一个时间步内的在某个方向上移动距离超过了该方向上模拟区域的尺寸,此时意味着原子之间受到了非常大的力,应当终止模拟,因为模拟系统出现了偏离物理实际的动力学行为。
。由周期性边界条件的这两个特点可知,非键结力的截断半径的大小不能超过模拟区域最小尺寸一半。此外,在实际分子动力学模拟中,当某个原子一个时间步内的在某个方向上移动距离超过了该方向上模拟区域的尺寸,此时意味着原子之间受到了非常大的力,应当终止模拟,因为模拟系统出现了偏离物理实际的动力学行为。