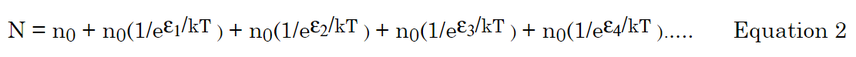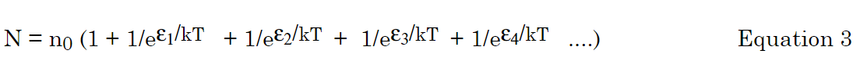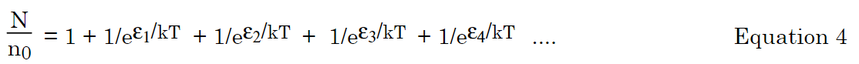通俗讲解：配分函数

配分函数是统计物理学中的核心工具，它本质上是一个“微观状态的统计计算器”。它的目的是将所有可能的微观状态（如粒子的位置、速度、能量等）的权重求和，再通过这个总和导出宏观热力学性质（如温度、压强、熵等）。简单来说，配分函数是连接微观粒子行为与宏观物理规律的数学桥梁。

对体系中一个粒子的所有可能状态的玻尔兹曼因子(所有量子态的有效值)求和，又称为状态和。

例如状态1*玻尔兹曼因子1+状态2*玻尔兹曼因子2+......状态n*玻尔兹曼因子n，得到了一个总的状态和，这个不是我们传统理解的状态1个数+状态2个数+......状态n个数。因为微观世界不是固定的，是会在不同位置进行分布的，所以都存在概率问题，也就是不会有不同的状态。

 extension://ngbkcglbmlglgldjfcnhaijeecaccgfi/https://www2.chem.umd.edu/groups/alexander/chem481/PartitionFunction.pdf

方程1中N为总的粒子数目，n0为基态数目，n1为第一激发态数目

在玻尔兹曼分布中，第一激发态的粒子数是基态粒子数的一个分数，微观状态下需要考虑玻尔兹曼分布

这个时候把激发态的全部替换

提取公因式

所以配分函数Q=N/n0，所以大于1

所以这个配分函数纯粹只是推到出来的东西，玻尔兹曼统计只是以基态的概率为基准1推导，其他能级的概率与基态概率的比例关系（玻尔兹曼因子），但这样，比例和加起来是大于1的，而粒子出现在各个能级的总概率为1，所以为了进行归一化处理，把这些所以的比例加起来，作为分母，这也是为什么配分函数的值与基态概率互为倒数的原因。

通俗类比：

假设你有一袋骰子，每个骰子的点数可能为1到6。如果同时抛1000枚骰子，所有可能的点数组合构成了一个“骰子宇宙”。配分函数的作用类似于统计所有可能的骰子组合总和，并从中计算出平均点数、点数分布等宏观信息。

骰子的总点数对应系统的总能量；

骰子的不同点数组合对应微观状态；

配分函数就是所有可能点数的“加权总和”，最终通过这个总和计算平均点数（类似温度或压强）。