*欢迎大家去观看原文，并引用

标题：Effective Control of Thermal Transfer in Nanoconfined Water byApplying an Electric Field: A Molecular Dynamics Study

期刊：J. Phys. Chem. B

网址：https://doi.org/10.1021/acs.jpcb.5c00928

一、文章摘要

在纳米尺度下所封闭的水的热学性质与普通水有所不同。当施加电场时，水分子的运动状态会发生变化，这会影响纳米封闭水中的热传递。为了探究这一现象，我们进行了分子动力学模拟，以研究在均匀电场作用下纳米通道中封闭水的热传递情况。研究结果表明，当电场强度在平行于纳米通道固体-液体界面的方向下低于4 V nm−1，或者在垂直于该界面的方向下低于9 V nm−1时，纳米封闭水的热导率会降低。这种降低归因于电场力导致的水分子热扩散受限。相反，当电场强度超过4 V nm−1 或9 V nm−1时，由于强电场的作用，水分子会冻结，从而导致纳米封闭水的热导率大幅增加。界面热阻在热源一侧会降低，而在冷源一侧则会随着电场强度的增加而增大。此外，将电场平行于纳米通道施加使用能够更有效地促进水分子的电致冻结，从而在纳米受限的水中实现更显著的热传输增强。

二、计算图文

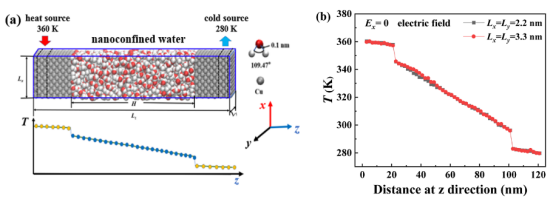
图 1.（a）初始模拟系统的模型：红色、白色和灰色的粒子分别代表氧原子、氢原子和铜原子。 （b）具有不同横截面积的两个纳米通道的温度分布。

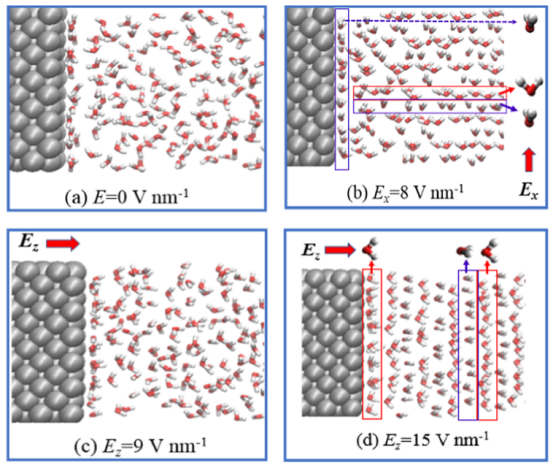
图2. 在不同电场作用下，界面处及水体内部水分子的分布情况。

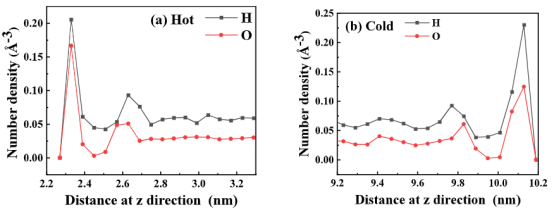
图3. 在无电场的情况下，靠近（a）高温表面和（b）低温表面的氧原子和氢原子的密度分布。

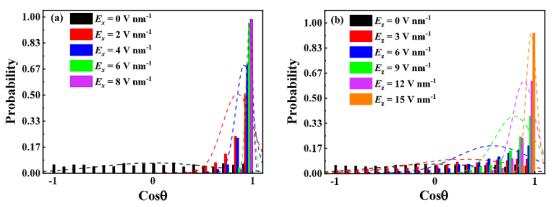
图4. 在不同强度的（a）x 方向和（b）z 方向电场作用下水偶极子的概率分布。

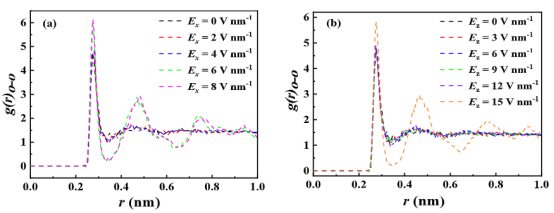
图 5.在（a）沿 x 方向和（b）沿 z 方向作用下不同强度电场的作用下，水中氧原子的 RDF（径向分布函数）。

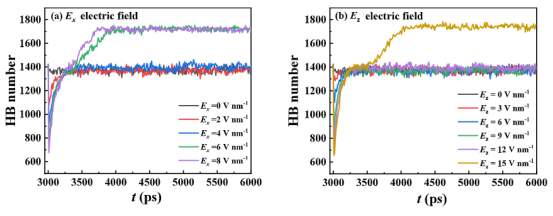
图6. 在（a）x 方向（b）z 方向均匀电场作用下纳米受限水的氢键数量

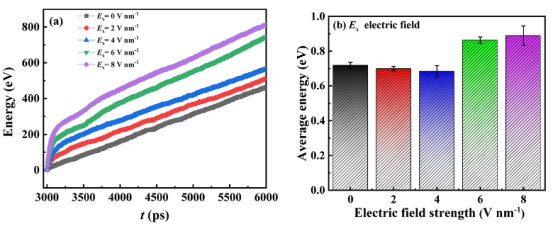
图8. （a）能量随时间的变化曲线。 （b）在正 x 方向的电场作用下，冷源和热源处能量变化的平均值。

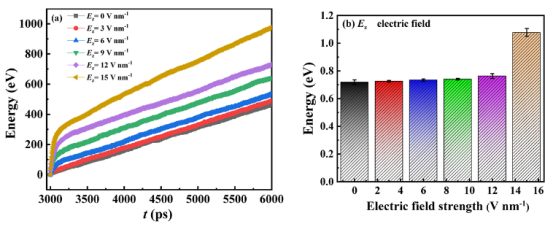
图9. （a）能量随时间的变化曲线。 （b）在正 z 方向的电场作用下，冷源和热源处能量变化的平均值。

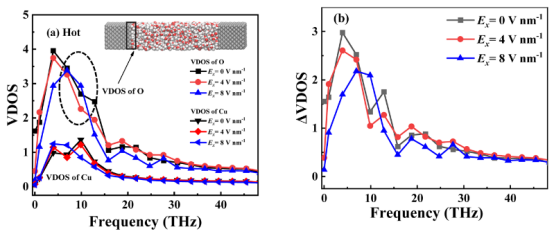
图15. （a）铜原子与氧原子的 VDOS 图谱。 （b）在正 x 方向的电场作用下，铜 -水界面处铜原子与氧原子之间的 VDOS差值（热源侧）。

三、计算分析

3.1电场方向与强度对水分子的调控机制

分子取向分布（图4）：计算偶极矩与电场方向的夹角概率分布，量化电场诱导的分子定向排列。结果显示平行电场（Ex=8 V/nm）或垂直电场（Ez=15 V/nm）可使水分子完全定向。

相变临界阈值：通过径向分布函数（RDF）（图5）和氢键数量统计（图6）识别电致冻结（electro-freezing）的临界场强（Ex=6 V/nm，Ez=15 V/nm）。RDF峰值的显著增高（4.73→6.01）及氢键数量跃升证实了晶体结构的形成。

界面吸附层密度（表2-3）：统计第一吸附层水分子数密度，发现平行电场增加密度，垂直电场因分子重排导致密度下降。

3.2热输运特性的调控规律

热导率非单调变化（图10-11）：计算热通量（公式3）和温度梯度（公式4），发现热导率在低电场（Ex<4 V/nm, Ez<9 V/nm）因分子扩散受限而降低，在高电场（Ex>6 V/nm, Ez=15 V/nm）因相变跃升52.56%（平行电场）和54.49%（垂直电场）。

界面热阻（ITR）的非对称响应（图7, 图13）：通过温度跳变（ΔT）和Kapitza长度（L_k）量化ITR。平行电场下热源侧ITR降低（L_k从11.29→7.13 nm），冷源侧升高（13.57→29.61 nm）。

3.3分子动力学行为的微观解释

扩散系数（图12）：通过均方位移（MSD）计算扩散系数（公式5），证实电场抑制分子运动（D从2.1×10⁻⁹→0.56×10⁻⁹ m²/s）。

声子谱匹配分析（图15-16）：计算Cu-O原子的振动态密度（VDOS）及其差值（DVDOS），解释ITR变化源于界面声子耦合增强（热源侧DVDOS峰值降低）。

3.4计算模型与实验体系的映射

参数实验校准

采用SPC/E水模型（文献36），其介电常数、扩散系数等参数经实验验证可复现液态水特性

Cu-H₂O相互作用参数（表1）基于金属-水界面接触角的实验数据优化，确保亲水性界面行为的真实性

实验现象复现验证

电场诱导分子取向（图2, 图4）：
模拟结果与Toney的X射线衍射实验（文献24）一致，证实界面水分子在电场下的定向排列规律

电致冻结临界场强：

5 V/nm阈值与Zangi的介电测量实验（文献30）吻合，支持模拟相变机制的可靠性

3.5热输运性质的实验可验证预测

热导率非单调变化

预测低电场下热导率下降（扩散受限）、高电场下跃升（相变增强）

可通过瞬态热反射法（TDTR）测量纳米通道热导率验证预测

界面热阻非对称响应

预测热源侧ITR下降（-36.8% @Ex=8V/nm）、冷源侧升高（+118%）

可通过泵浦-探测光谱测量固液界面温度跳变验证

3.6微观机制与实验表征的关联

结构-性能对应关系

氢键数量突增（图6）→ 拉曼光谱可检测O-H振动峰偏移

RDF晶体峰出现（图5）→ XRD可验证有序结构生成

声子耦合机制（图15）

预测的VDOS匹配优化（热源侧）与声子透射实验（文献50-51）原理相通

四、计算方法

4.1分子动力学模拟框架

模型构建

几何结构（图1a）：

铜板：厚度2.172 nm（12层FCC晶格，晶格常数0.362 nm），最外层固定。

纳米通道：尺寸2.2×2.2×12 nm³，宽度H=7.6 nm，含1200个水分子（SPC/E模型）。

边界条件：x/y方向周期性边界，z方向固定边界。

力场与势函数

截断半径：10 Å（短程力与长程库仑力均截断）。

长程库仑修正：PPPM（Particle-Particle-Particle-Mesh）算法。

关键参数（表1）：

混合规则：Cu-O参数通过Lorentz-Berthelot规则生成。

水分子约束

SPC/E模型：刚性水分子（固定O-H键长0.1 nm，H-O-H键角109.47°）。

约束算法：SHAKE算法（维持几何构型不变）。

4.2模拟流程细节

初始化与平衡

平衡阶段：

系综：NVT（恒温320 K）。

时间：2000 ps（2 ns）。

控温方式：Langevin热浴。

验证尺寸效应：

对比通道截面3.3×3.3 nm²（2700个水分子），温度分布一致（图1b），确认模型可靠性。

非平衡模拟

温度梯度设置：

热源：360 K（铜板顶部3层原子）。

冷源：280 K（铜板底部3层原子）。

控温方式：Langevin热浴（阻尼系数未明确，默认值1 ps⁻¹）。

电场加载：

均匀电场施加于x或z方向，力 Fi=qiE 直接作用于电荷。

数据采集：

弛豫时间：3000 ps（3 ns）达到稳态。

生产阶段：1000 ps（1 ns）统计结果。

时间步长：1 fs（飞秒级精度）。

4.3关键物理量计算方法

温度计算

切片处理：沿z方向以0.2 nm厚度分片计算局部温度。

热通量与热导率

热通量 J（公式3）：

Ecum：通过冷/热源的能量累积量（图8-9）。

热导率 λ（公式4）：

dT/dz：水膜中部线性温度梯度（避免界面振荡影响）。

界面热阻（ITR）

ΔTinterface：通过线性外推法确定界面温度跳变（图7）。

4.4结构动力学分析

径向分布函数（RDF）：

计算氧原子间距分布（图5），识别相变（峰值位置0.275 nm）。

氢键数量：

统计每个水分子形成的氢键（距离<3.5 Å，角度<30°）（图6）。

扩散系数 D（公式5）：

基于均方位移（MSD）计算（图12）。

声子谱分析

振动态密度（VDOS）（公式8）

聚焦3.96–5 THz关键频段（主导热传递）（图15）。

4.5计算工具与验证

软件平台：LAMMPS（Large-scale Atomic/Molecular Massively Parallel Simulator）。

算法：速度Verlet积分（时间可逆性保持）。

验证方法：

延长模拟至10 ns，确认4 ns后温度分布稳定（图7）。

对比无电场下热导率（0.780 W·m⁻¹·K⁻¹），与文献值（0.897–0.940 W·m⁻¹·K⁻¹）差异归因于铜壁约束。