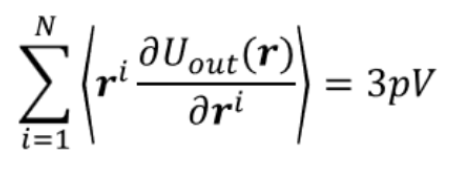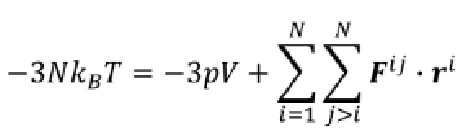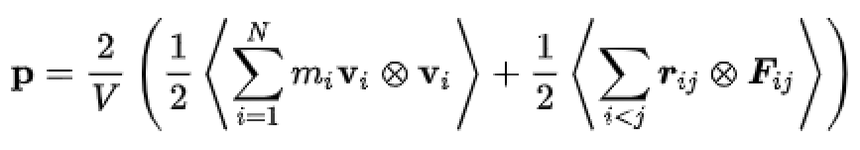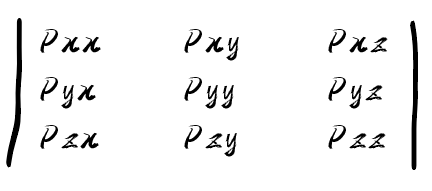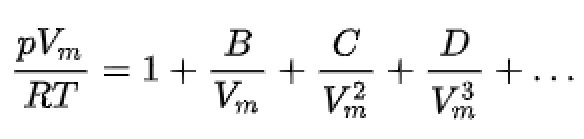|
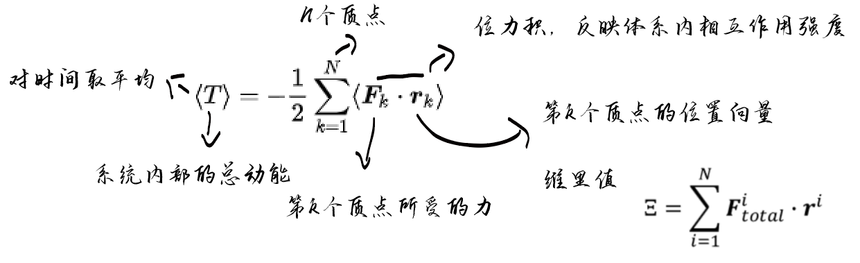
控压技术时间:2025-05-21 同样的我们首先需要先了解什么是压力 压力是描述系统内分子之间相互作用的力的总和 它是由于分子之间的碰撞和相互作用产生的 可以看作是对单位面积施加的力的量度 在分子尺度上,压力可以通过分子的动量变化和相互作用力来计算 计算压力时有一个词叫做位力定理(Virial theorem),有的书叫维里定理 1870年夏天,克劳修斯在一次报告中提到了“系统的平均活力等于其维里” 是力学中描述稳定的多自由度孤立体系的总动能和总势能时间平均之间的数学关系 考虑一个有N个质点的体系,其数学表达式为:
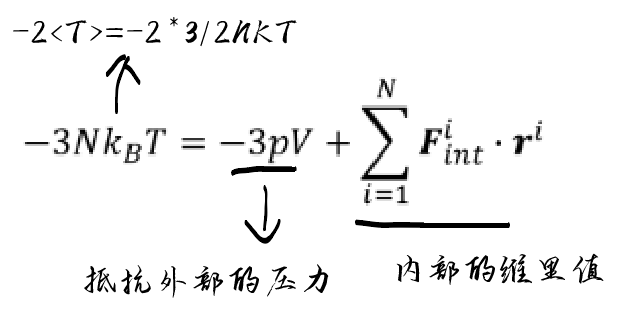
由于Fk是指的k点受到力,这个力包含内部分子间相互作用力及外部的压力 由于平衡内外压力一样,如果没有分子间的作用力,我们可以理解为压力是撞出来的 由于动量有3个自由度,所以需要考虑3个自由度 外部的功为3pv,等于抵抗产生的势能=外部做的功
代入维里方程-2<T>=<U> 维里是合力F与矢径的标积平均值之半 即以无穷远为零势点之势能绝对值之半;而活力是系统的总动能 <U>=内部势能-外部势能
当使用对势的时候
压强张量是一个描述系统各个方向上压强分布的张量 通常表示为一个3x3的对称矩阵,其中的元素表示各个方向上均方压强 压强张量的对角元素表示系统在各个方向上的压强 非对角元素表示不同方向上的相关压强
当P = Px = Pyy = Pz表现为同向异性压力 与位力定理名字比较像的一个词叫维里展开式(Ville unfolds) 两者看上去像,也有一定联系,我经常弄错,所以特意写出来,他们不是一个意思 假设有 N 个分子组成的系统,对于一个理想气体 根据分子动理论,分子之间表现出弹性碰撞 它们在相互作用力的瞬态作用下,沿着各个方向以各不相同的速度运动 根据统计力学的理论,可以推导出气体分子的总动能 与分子之间相互作用引起的平均势能之间的关系 并由此得到气体的Virial方程
由此也可推导理想气体方程PV=NRT 维里方程更符合实际 Vm是气体分子的摩尔体积,计算式:Vm=V/n R是气体常数 B表示每两个分子间的相互作用 C表示每三个分子间的相互作用 以此类推, 如果考虑的项数越多,方程的精确性就越高 BCD只是关于温度的函数 Berendsen控压技术,与它的控温思路是一样的,加入一个耦合参数控制压力变化速度 根据前面的位力定理我们知道P~r有关系,所以通过耦合参数,调整压缩系数, 再通过压缩系数调整r,就是原子的位置, 该方法对于P控制不够精确,不能产生正确的NPT,所以相比控温可用,控压尽量不用 C-rescale控压技术与Bussi-Parinello-velocity rescaling热浴思路类似 具有时间常数 tau-p 的指数松弛压力耦合, 包括一个随机项以强制执行正确的体积波动 每个控压步骤都会缩放盒子,它可以用于平衡和最终模拟 Parrinello-Rahman控压技术与Nosé-Hoover热浴思路类似 容易振荡,所以没有办法用在平衡后的采样中 |