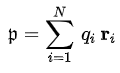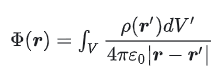|
通俗讲解:偶极矩时间:2025-05-18 在电磁学里,有两种偶极子(英语:Dipole): 电偶极子是两个分隔一段距离,电量相等,正负相反的电荷。 磁偶极子是一圈封闭循环的电流。例如一个有常定电流运行的线圈。 偶极子的性质可以用它的偶极矩描述。
电偶极矩由负电荷指向正电荷,大小等于正电荷量乘以正负电荷之间的距离。
偶极矩是衡量分子或电荷系统极性大小的物理量,定义为正、负电荷中心间的距离(d)与电荷量(q)的乘积,数学表达式为 μ = q × d。它是一个矢量,方向从正电荷中心指向负电荷中心,常用单位是德拜(D)或库仑·米(C·m)。
极性判断:若分子正负电荷中心重合(如二氧化碳),偶极矩为0,属于非极性分子;若不重合(如水),则偶极矩不为0,属于极性分子。 几何构型分析:通过偶极矩的数值和方向,可以推断分子的空间结构(如直线型、折线型)。
一、目的与意义偶极矩的核心目的是揭示分子或材料的电学性质,具体应用包括:
分子结构研究:判断分子的几何形状和对称性(如区分CO2的直线型与H2O的折线型)。 材料设计:指导液晶材料、介电材料等极性材料的开发。 药物开发:预测药物分子与靶点蛋白的相互作用位点。 化学反应预测:分析分子间作用力(如范德华力、氢键)对溶解性、沸点的影响。
二、测量与计算实验测量:溶液法:通过测量溶液的电容、密度等参数推算偶极矩(如将药物溶解在环己烷中测试)。 光学法:利用分子在电场中的极化响应(如红外光谱分析振动引起的偶极矩变化)。 理论计算:量子化学软件(如Gaussian):通过优化分子几何结构,计算电子密度分布和偶极矩矢量。
量子力学的电偶极子算符试想一群粒子,数量为 N,电荷量和位置分别为 qi和 ri,i=1,2,…,N。例如,这个群集可能是一个分子,由电荷量为 −e的电子,和电荷量为 eZj的原子核所构成;其中,Zj是第 j个原子核的原子序。这个群集的电偶极子的量子算符p是
电势的多级展开如果一个电荷系统集中于一个小区域V,他在空间中的电势为: 如果该分布可积,那么我们只要知道了电荷分布密度ρ(r’)就可以计算得到空间的电势和电场强度。但是很多情况下,很多是无法积出的,譬如不规则的物体。但是,如果我们将电荷仅局限于一个很小的空间,并且在一个远离电荷区域的地方测量,即其r远大于区域V的线度,这时候我们就可以不选取严格积分,可以利用级数展开。 偶极矩是描述电荷分布的物理量,通常是由一对等量异号电荷形成的。在两个都是正电荷或负电荷的情况下,偶极矩的概念并不适用,因为没有形成偶极。偶极矩的方向是从负电荷指向正电荷。 如果你有两个相同的正电荷或负电荷,它们之间的相互作用会导致静电力,但不会形成偶极矩。偶极矩主要用于描述存在电荷分离的情况,即一个电荷正一个电荷负的情形。对于两个相同电荷,你可以考虑它们的电场和相互作用力,而不是偶极矩。 |