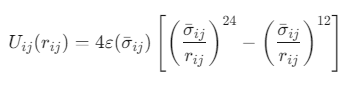|
硅酸钙水化物的多尺度力学行为:实验与粗粒度计算的见解时间:2025-07-07
*欢迎大家去观看原文,并引用 标题:Multiscale Mechanical Behavior of Calcium Silicate Hydrates:Insights from Experiments and Coarse-Grained Computation 期刊:ACS Appl. Mater. Interfaces 网址:https://doi.org/10.1021/acsami.4c22154
一、文章摘要探究纳米颗粒聚集的机械机制是推进纳米结构材料科学的关键;然而,由于涉及从分子尺度到数百纳米范围内的复杂分子行为和排列结构,这一研究极具挑战性。在本文中,我们研究了胶凝纳米颗粒(C-S-H胶体)强度的来源。我们对脱钙硬化水泥浆进行了统计压痕分析,以解读 C-S-H 分子及其有效相互作用的机械信息。然后,这些分子层面的属性作为粗粒度计算聚集的 C-S-H颗粒簇拉伸特性的参数参考。结果揭示了 C-S-H集团的纳米级行为,包括排列构型、应力-应变关系、应力空间分布和断裂情况,并为分子相互作用和排列构型如何影响 C-S-H胶体的机械行为提供了见解。单/多界面和孔隙/裂缝作用下的载荷传递机制是多尺度之间巨大机械差异的基础。
二、计算图文
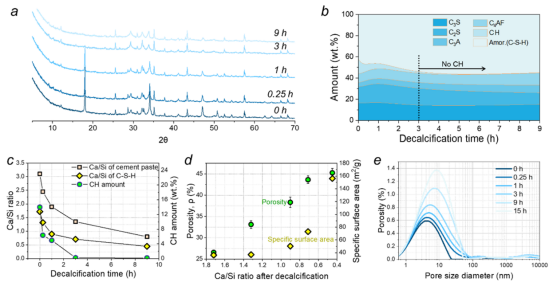
图 1.对硬化水泥浆体脱钙效应的多尺度表征。化学成分测量:(a)X射线衍射图谱,(b)水泥矿物与水化产物的质量比,(c)硬化水泥浆体中的钙/硅比以及 C-S-H凝胶。微观结构测量:(d)孔隙率和比表面积,以及(e)孔隙尺寸分布。
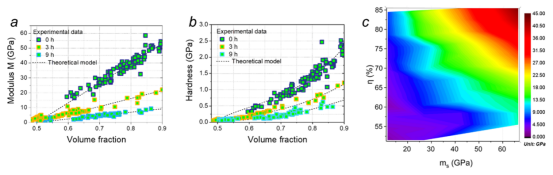
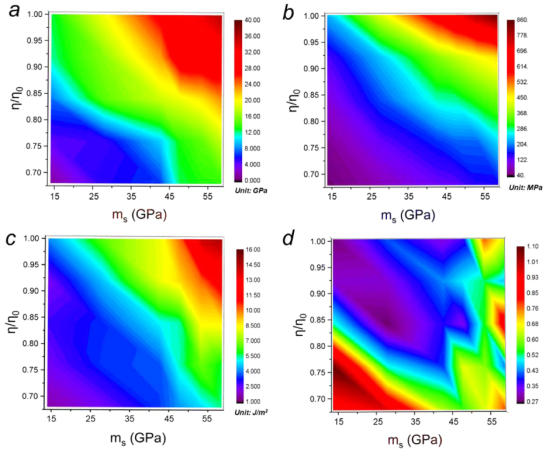
图 2.硬化水泥浆体脱钙后的力学性能:(a)压痕模量,(b)硬度,以及(c)随着体积分数η 和分子刚度 ms 的变化而变化的压痕模量。理论模型见公式4。
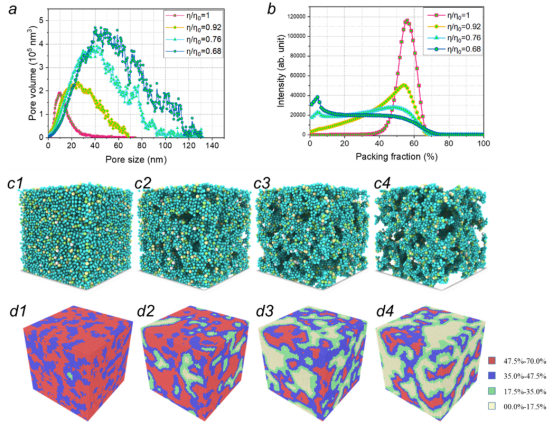
图 3.考虑凝胶收缩的微观结构演变计算。(a)孔隙尺寸分布,(b)局部填充率ηlocal,(c)填充构型,以及(d)ηlocal 的空间分布。凝胶收缩会导致微观结构重组和填充率降低,而标准化填充率η/η0 分别为(c1,d1)0、(c2,d2)0.92、(c3,d3)0.76 和(c4,d4)0.68。图 d 中的颜色表示ηlocal。
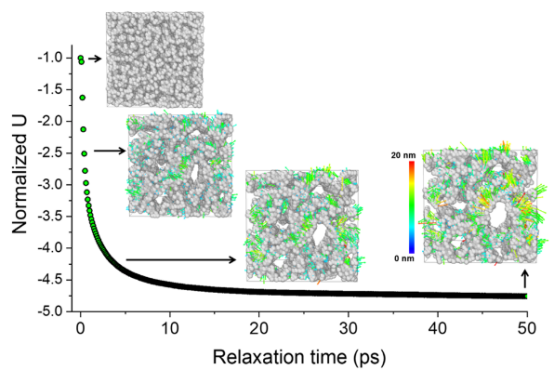
图 4.在胶体收缩作用下,随着结构松弛,η/η0 =0.68时的势能随时间变化曲线。彩色箭头表示位移矢量,其大小用不同的颜色表示。紧密堆叠的结构转变为环状结构。
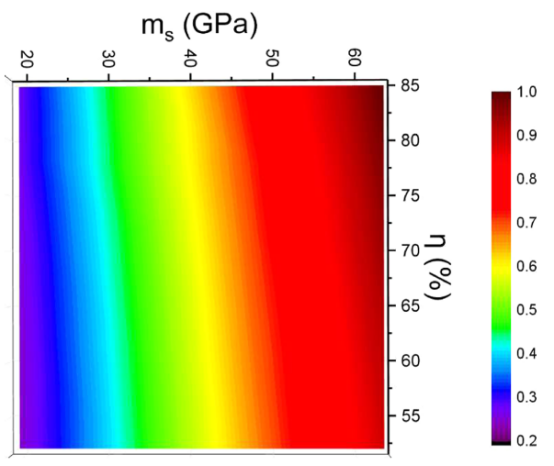
图5. C−S−H胶凝体排列结构的归一化势能随分子刚度 ms 和排列系数η 的变化关系。
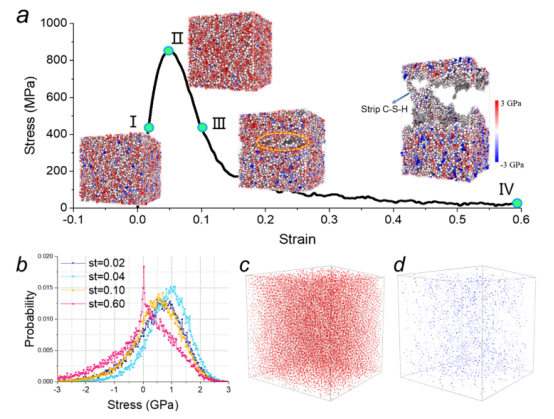
图6.原始样品的纳米级拉伸行为计算结果(ms =57.5 GPa,η/η0 =1)。(a)应力-应变关系图。插入了样品在弹性阶段、峰值顶部、峰值后以及破坏阶段的瞬态图像,其中颜色表示沿伸长方向的碳-硅-氢颗粒上的应力。图中的黄色圆圈标记了裂纹位置,此处应力接近零。(b)不同应变(st)下碳-硅-氢颗粒上的应力分布。(c,d)在应变值为0.04时的应力空间分布。正值(红色)表示拉伸应力,负值(蓝色)表示压缩应力。
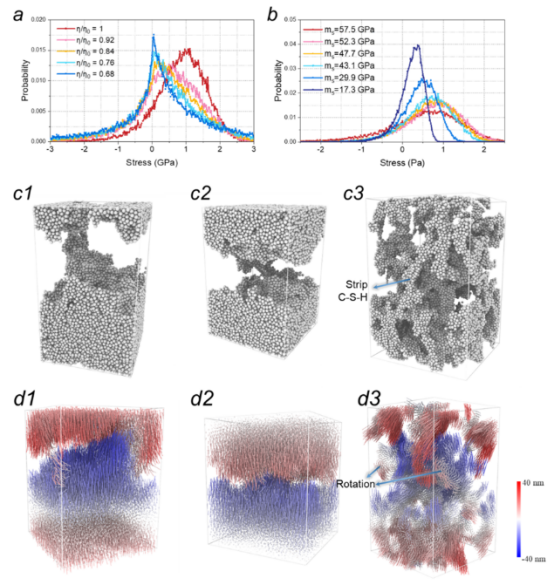
图 7.具有疏松孔隙结构或低 MI 的 C−S−H凝胶的拉伸性能。对于不同(a)η 和(b)ms 的样品,在应力-应变曲线峰值顶部沿拉伸方向的晶粒应力统计数据。(c)破坏阶段的快照图和(d)样品中晶粒的位移矢量,其中(c1,d1)ms =57.5 GPa,η/η0 =1,(c2,d2)ms =17.3 GPa,η/η0 =1,以及(c3,d3)ms =57.5 GPa,η/η0 =0.68。颜色表示位移矢量的方向,正向表示向上。
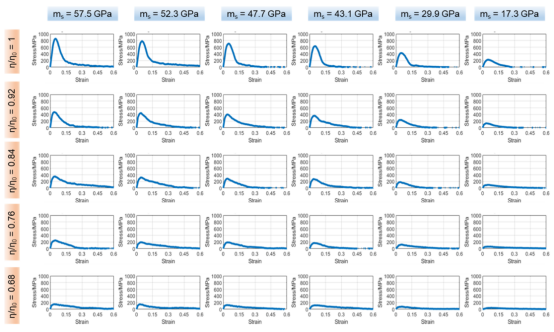
图8.纳米级 C-S-H凝胶的应力-应变关系。
图 9.计算了由 ms 和η 的衰减所导致的 C−S−H凝胶在纳米尺度上的力学性能变化,包括(a)杨氏模量、(b)拉伸强度、(c)断裂能以及(d)断裂应变。
三、计算分析文章利用粗粒化计算(CG)模拟C-S-H凝胶的纳米尺度行为,重点关注分子相互作用(Molecular Interaction, MI)和堆积分数(packing fraction, η)对机械性能的影响。模拟内容涵盖以下几个方面:
3.1孔隙结构与堆积配置演化通过CG模型模拟脱钙导致的C-S-H凝胶收缩(gel shrinkage),分析孔隙大小分布、局部堆积分数(η_local)和空间配置的变化。 结果显示,凝胶收缩引发颗粒迁移和重组,导致孔隙率增加和微结构粗化(从致密结构转变为网状交联凝胶簇)。孔隙阈值从20nm增至50nm,与实验数据(如NMR和氮吸附)一致。 关键发现:MI衰减(分子刚度下降)对孔隙结构无显著影响,但η下降主导微结构粗化,中断力传递路径,降低机械性能。
3.2分子相互作用(MI)对系统能量的影响模拟MI衰减(通过降低Lennard-Jones势的阱深ε实现),量化其对系统势能的影响。结果显示,MI主导凝胶解体能量,但几乎不改变堆积纹理(如孔隙分布)。 势能计算公式:广义Lennard-Jones势描述颗粒间相互作用。 关键发现:孔隙/裂纹区域能量趋近于零,突显裂纹作为失效起点的危害。
3.3纳米尺度拉伸行为与断裂机制模拟单轴拉伸测试(应变率0.08/ps),分析应力-应变关系、应力空间分布及断裂能量。结果显示C-S-H凝胶的拉伸行为包括弹性阶段、屈服阶段和失效阶段。 重点揭示: 致密结构(η/η₀=1)下,应力均匀分布,断裂面平坦;多孔结构(η/η₀=0.68)下,应力集中导致断裂面粗糙,韧性提高。 分子刚度(mₛ)衰减降低颗粒极限承载能力(从3GPa降至<1GPa)。
3.4机械性能参数化依赖关系量化η和mₛ对Young's模量、抗拉强度、断裂能量和断裂应变的影响(图9)。结果显示: η和mₛ共同衰减导致模量、强度和断裂能量下降。 η对抗拉强度影响更大(权重较高),mₛ对断裂应变影响更显著。
3.5尺寸效应与可重复性验证分析凝胶尺度扩大时的尺寸效应:松散结构下机械性能随尺度增加而下降,致密结构下变化不显著(归因于孔隙/裂纹连通)。 通过多次运行验证可重复性(初始结构、参数和代码不变),结果完全一致(图S1)。
四、计算方法4.1计算方法框架文章采用粗粒化分子动力学(CGMD) 与 蒙特卡洛(GCMC) 相结合的方法,通过LAMMPS软件实现。整体流程如下: 4.1.1. 模型构建与初始化初始结构生成使用 Grand Canonical Monte Carlo (GCMC) 模拟C-S-H凝胶沉淀过程: 每个循环:进行 NMC 次颗粒插入/删除尝试 → 随后进行 NMD=100 步分子动力学弛豫(正则系综)。 终止条件:颗粒数量变化 <10/10000步(达到稳定堆积状态)。 模拟盒尺寸:150×150×150nm3。 颗粒尺寸:6–9 nm(基于SANS测量数据[s11-s14]),符合C-S-H凝胶的纳米颗粒特征。
相互作用势设置广义Lennard-Jones势(用于描述C-S-H颗粒间作用力):
rij:颗粒间距离(平衡距离 r0=21/12σij) σij=(σi+σj)/2:平均颗粒直径 ε:势阱深度(与分子刚度 ms关联) γ=12(基于AFM测量)
4.1.2. 关键参数设置依据
注:η0=50% 为渗流阈值(低于此值无强度)[s17]。
4.1.3. 模拟过程结构弛豫:在等温等压系综(NPT)下弛豫至平衡状态(压力=0,室温)。 脱钙效应模拟:分子相互作用衰减:降低 ε 使 ms 从57.5 GPa梯度降至17.3 GPa(对应Ca损失)。 凝胶收缩:减小颗粒直径 σ,使 η/η0 从1.00降至0.68(模拟脱钙致密化损失)。
4.1.4. 性能计算孔隙结构分析:离散化方法:将模拟盒划分为1000×1000×1000网格单元,识别固体/孔隙区域。 局部堆积分数:以每个网格点为中心,计算10 nm半径球体内的η_local。 比表面积:基于颗粒集构建多面体网格(参考Stukowski算法),计算凝胶内/外表面。 归一化处理:为避免争议,使用η_local归一化值(基于实验比表面积和孔隙率校准)。
拉伸测试:模拟设置:在LAMMPS中进行单轴拉伸,沿a轴逐步拉伸(应变率0.08/ps),正则系综(NVT)下输出应力和位移。 应力-应变分析:记录box应力,绘制曲线以提取Young's模量、抗拉强度和断裂应变。 断裂能量。 位移分析:基于颗粒坐标计算位移矢量,可视化裂纹扩展路径。
势能计算:系统总势能作为MI和η的函数(图5)。
4.2验证与参数敏感性可重复性:固定初始结构、输入参数和代码,多次运行比较结果(图S1)。 尺寸效应测试:将模拟盒扩大至2×2×2, 4×4×4, 6×6×6倍,分析尺度对机械性能的影响。 敏感性分析:通过梯度变量(η和mₛ)量化参数对机械性能的权重(图9)。
4.3实验-模拟一致性验证孔隙分布:模拟孔隙大小分布与实验LF-NMR数据匹配(对比文档2图3a与图1e)。 模量演化:模拟模量-η关系与纳米压痕实验一致(对比文档2图9a与图2c)。 分子强度:模拟颗粒间极限抗拉强度(2.5–3 GPa)与MD结果(2.2–4 GPa)吻合。
|