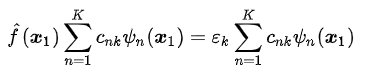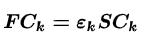|
通俗讲解:Roothaan方程时间:2025-05-13 Roothaan方程是量子化学中用于求解多电子体系波函数的核心数学工具,其本质是将复杂的Hartree-Fock积分微分方程转化为矩阵形式的代数方程,从而通过计算机进行高效计算。我们通过一个通俗案例来理解其核心思想和应用场景。
一、通俗案例:拼图游戏的“模块化重组”假设你有一幅复杂拼图(多电子体系),传统方法需要同时调整所有碎片的位置(直接求解多体方程),计算量巨大。而Roothaan方程的思路类似于: Ø 拆分拼图块:将整幅图拆分为标准形状的模块(如基函数:高斯函数或斯莱特型原子轨道)。 Ø 重组模块:通过调整每个模块的方向和位置(基函数组合系数),逐渐逼近完整图案(真实波函数)。 Ø 迭代验证:每次重组后检查是否匹配(计算能量是否收敛),直到误差小于阈值。 Ø 类比到量子化学: u 拼图模块 → 基函数(如氢原子的1s轨道) u 重组规则 → Roothaan方程的矩阵运算 u 验证迭代 → 自洽场(SCF)循环
二、Roothaan方程的科学本质1. 数学形式与目的Roothaan方程的核心公式为: FC=SCϵ
F:Fock矩阵(包含单电子动能、核吸引能、电子间平均排斥能) S:基函数重叠矩阵(衡量不同基函数的重叠程度) C:系数矩阵(描述分子轨道如何由基函数线性组合而成) ε:轨道能量矩阵 目的:通过代数运算代替微积分计算,将Hartree-Fock方程的非线性问题转化为可解的广义特征值问题。 可以通过调整系数得到自己想要的结果 2. 关键步骤以氢分子(H₂)为例:
Ø 选择基组:例如两个氢原子的1s轨道作为基函数(模块)。 Ø 构建Fock矩阵:计算基函数间的单电子积分(核吸引、动能)和双电子积分(排斥能)。 Ø 正交化处理:通过Lowdin方法将非正交基组转换为正交基组,简化方程形式。 Ø 迭代求解:通过自洽场循环调整系数矩阵C,直到能量收敛(通常迭代5-10次)。
三、为何需要Roothaan方程?1. 解决计算瓶颈Hartree-Fock方程原本是积分微分方程,需计算大量复杂积分(如双电子积分),直接求解几乎不可能。Roothaan方程通过基组展开,将问题转化为矩阵运算,显著降低复杂度。
2. 实际应用场景分子轨道计算:如氧气(O₂)的磁性预测需考虑自旋极化基组。 材料模拟:半导体能带结构的初步计算常以Roothaan方程为起点。
3. 局限性基组依赖性:基函数的选择(如高斯型或斯莱特型)直接影响计算精度。 正交化误差:非正交基组需额外转换步骤,可能引入近似误差。
四、改进与扩展1. 正交化方法如Lowdin对称正交化,通过矩阵分解(如S⁻¹/²)将重叠矩阵S转换为单位矩阵,简化方程为标准特征值问题。 示例公式: 2. 密度矩阵加速通过密度矩阵(D)快速更新Fock矩阵,减少双电子积分计算次数。
总结Roothaan方程如同量子化学的“模块化编程”,将多体问题拆解为基函数组合的矩阵运算,为分子模拟提供实际可行的计算路径。尽管受限于基组选择和迭代效率,它仍是现代量化计算(如密度泛函理论)的基础框架 |