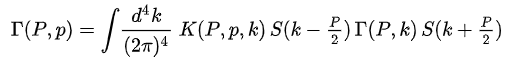|
通俗讲解:Bethe-Salpeter方程(BSE)时间:2025-05-13 Bethe-Salpeter方程(BSE)是量子力学中描述两个粒子间复杂相互作用的数学工具,尤其用于研究它们如何形成束缚态(如介子、激子等)。其核心思想是:通过考虑所有可能的相互作用路径(包括反复碰撞、能量交换等),精确计算粒子的集体行为,而不仅仅是单次碰撞的效果。
通俗类比: 想象两个人在拥挤的舞池中跳舞(类比粒子相互作用),传统方法只能计算他们偶尔碰到对方的概率(如薛定谔方程),而BSE则考虑了他们反复推搡、跟随音乐节奏调整动作的所有可能路径,最终预测两人是形成稳定的“双人舞”(束缚态)还是分开。
Bethe-Salpeter方程(BSE)于1951 年首次推导出来并应用于粒子物理学和QED。BSE在固体中的首次应用是由Hanke和Sham完成的,他们计算了块状硅的吸收光谱,与实验定性一致。从那时起,许多工作都表明 BSE 在描述材料光学特性方面的成功应用,BSE 已成为吸收光谱从头模拟的最新技术。
Bethe-Salpeter 方程是四点极化函数的类似戴森方程L(1,3,2,4),这可以通过汇总无限级非相互作用的偏振函数来找到L0(1,3,2,4),通过相互作用找到内核连接Ξ(6,5,7,8)
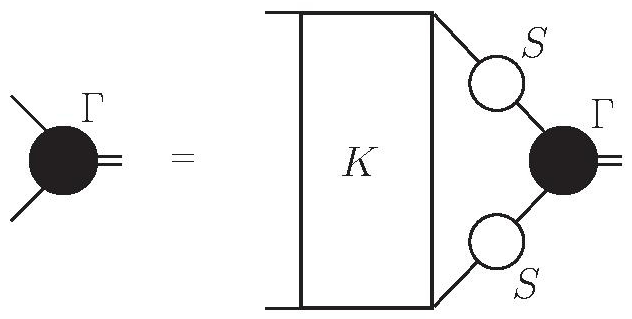
极化率函数的 Bethe-Salpeter 方程的图示表示. B-S方程有许多不同形式,常用于粒子物理学的一种形式是:
其中Γ是Bethe-Salpeter振幅,K是相互作用,S是两个参与粒子的传播子。
|