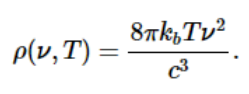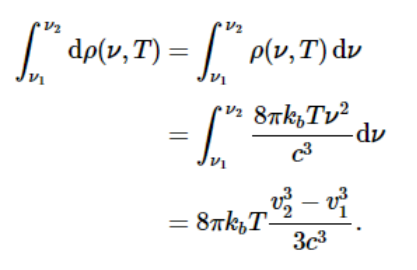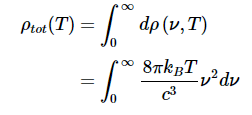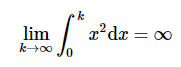|
1.1:黑体辐射不能用经典来解释时间:2025-05-19 学习目标经典物理学无法充分解释的一种实验现象是黑体辐射。本节的目标包括 l 熟悉黑体发射器 l 应用 Stefan-Boltzmann 定律估算发射器的总光输出 l 应用 Wien 位移定律来估计黑体发射器输出的峰值波长(或频率) l 了解 Rayleigh-Jeans 定律以及它如何无法正确模拟黑体辐射
所有温度高于绝对零度的正常物质都会发出电磁辐射,这代表了物体内部热能转化为电磁能的过程,因此被称为热辐射。相反,所有正常物质都会在一定程度上吸收电磁辐射。吸收落在其上的所有波长辐射的物体称为黑体。当黑体处于均匀温度时,其发射具有取决于温度的特征频率分布。这种发射称为黑体辐射。 室温黑体呈黑色,因为它辐射的大部分能量是红外线,人眼无法感知。由于人眼无法感知较低频率的光波,因此在黑暗中以最低的微弱可见温度观察黑体,即使其客观物理光谱在红外范围内达到峰值,也会主观地呈现为灰色。当它变得有点热时,它就会呈现暗红色。随着温度的进一步升高,它会变成黄色、白色,并最终变成蓝白色。
图 1.1.1 :黑体辐射。加热时,所有物体都会发射电磁辐射,其波长(和颜色)取决于物体的温度。温度相对较低的物体(如铁匠锻造的马蹄铁)显示为红色,而温度较高的物体(如太阳表面)则显示为黄色或白色。 黑体辐射具有特征性的连续频谱,在实验上仅取决于身体的温度。事实上,我们可以更精确:物体在给定的温度和频率下发射的辐射与吸收相同辐射的辐射完全相同。 古斯塔夫·基尔霍夫 (Gustav Kirchhoff) 证明了这一说法:关键是,如果我们假设一个特定的物体吸收得比它发出的要好,那么在一个装满相同温度的物体的房间里,它吸收其他物体的辐射比辐射回给它们要好。这意味着它会变得更热,而房间的其余部分会变得更冷,这与热力学第二定律相矛盾。因此,物体在给定温度和频率下发射的辐射必须与吸收相同辐射的辐射完全相同,才能不违反热力学第二定律。 任何温度高于绝对零度的物体都会在一定程度上辐射,辐射的强度和频率分布取决于物体的详细结构。要开始分析热辐射,我们需要具体说明进行辐射的物体:最简单的情况是一个理想化的物体,它是一个完美的吸收器,因此(从上面的论点来看)也是一个完美的发射器。 那么,我们如何在实验室中构建一个完美的吸收器呢?1859 年,基尔霍夫 (Kirchhoff) 有一个好主意:在大盒子的侧面开一个小孔是一个很好的吸收器,因为任何穿过这个孔的辐射都会在内部反弹,每次反弹都会吸收很多辐射,并且几乎没有机会再次流出。所以,我们可以反过来做这件事:有一个侧面有一个小孔的烤箱,据推测,从孔中射出的辐射与我们将要找到的完美发射器一样好(图 1.1.2 ).
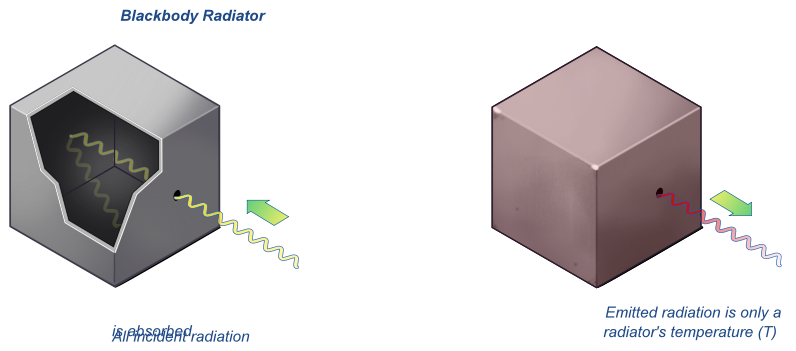
图 1.1.2 :黑体辐射体是任何具有完美发射器和完美辐射吸收体的物体。 到 1890 年代,实验技术已经得到充分改进,可以对黑体辐射的能量分布进行相当精确的测量。1895 年,在柏林大学,Wien 和 Lummer 在一个完全封闭的烤箱的侧面打了一个小孔,然后开始测量传出的辐射。从孔中射出的光束通过衍射光栅,该光栅将不同的波长/频率发送到不同的方向,全部朝向屏幕。探测器沿着屏幕上下移动,以查找在每个频率范围内发射的辐射能量。他们发现辐射强度/频率曲线接近图 1.1.3 中的分布 .
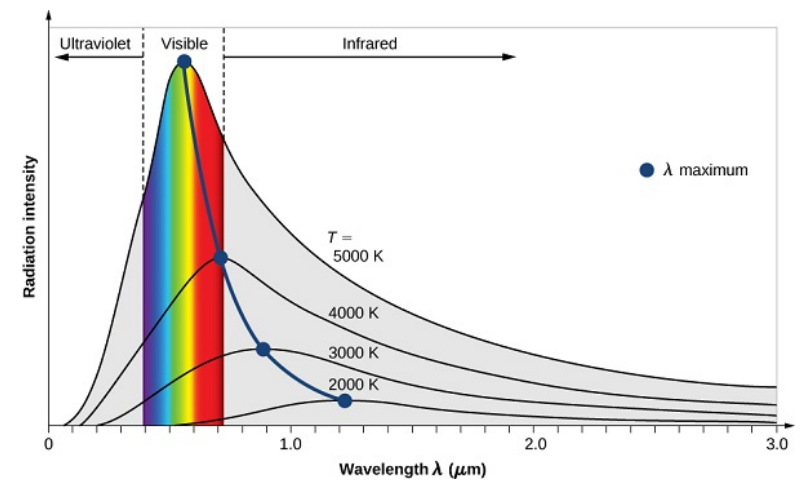
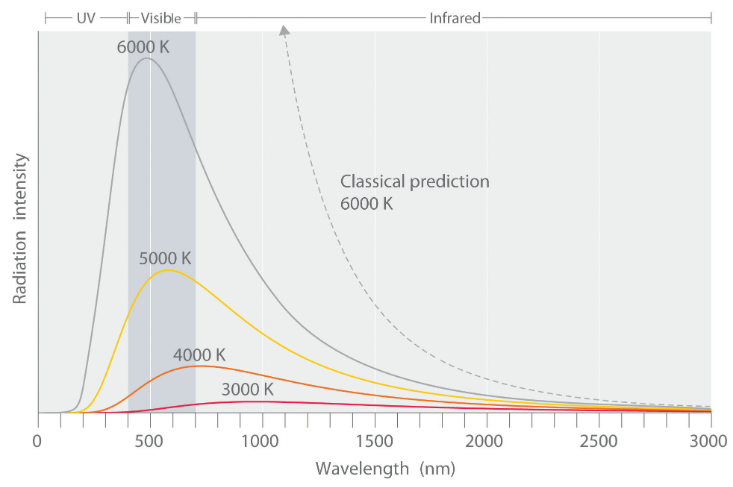
图 1.1.3 : 不同温度下黑体辐射光谱分布的图形表示。斯特凡-玻尔兹曼定律是发射幅度随温度升高而增加,维恩位移定律是随着温度升高而向较小波长的偏移。 通过测量不同温度下的黑体发射曲线(图 1.1.3 ),他们还能够构建两个重要的现象学定律(即,根据实验观察而不是根据自然的基本原理制定):斯特凡-玻尔兹曼定律和维恩位移定律。
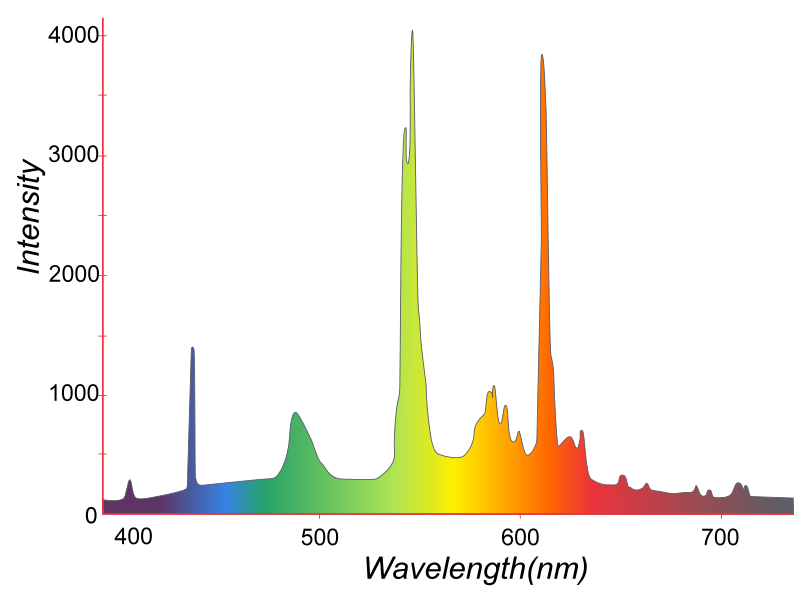
并非所有发射器都是黑体发射器黑体发射器的辐射是由材料的热活动产生的,而不是材料的性质,也不是它如何被热激发的。黑体的一些示例包括白炽灯泡、星星和热炉顶。发射显示为连续光谱(图 1.1.3 ) 替换为多种共存的颜色。但是,并非每个发射器都是黑体发射器。例如,荧光灯泡的发射不是一个。下面的光谱显示了荧光灯管的光分布,与图 1.1.3 中的连续光谱相反,它是不同光波长的离散波段的混合物 用于黑体发射器。
具有发射峰的荧光照明光谱。可见光谱中的强度(计数)与波长 (nm) 的关系图。
荧光灯泡含有惰性气体(通常是氩气和氖气)的混合物以及一滴低压汞。可见颜色的不同混合混合产生一种光,在我们看来是白色的,具有不同的阴影。
斯特凡-玻尔兹曼定律第一个基于实验观察的定量猜想是 Stefan-Boltzmann 定律 (1879),它说明了总功率(即,在图 1.1.3 中对所有发射频率的积分) )是绝对温度的四次方(图 1.1.4 ):
这里 P是物体每平方米发出的辐射总量 ( W atts/m2) σ是一个称为 Stefan-Boltzman 常数 ( 5.67×10−8W attsm−2K−4) T是对象的绝对温度(单位为 K) 通过比较图 1.1.3 中实验黑体辐射分布的积分值(即曲线下),可以很容易地观察到斯特凡-玻尔兹曼定律 在不同温度下。1884 年,玻尔兹曼推导出了这一点T4行为从理论出发,将经典的热力学推理应用于一个装满电磁辐射的盒子,使用麦克斯韦方程组将压力与能量密度联系起来。也就是说,从孔中流出的微量能量(图 1.1.2 ) 当然与内部的辐射强度具有相同的温度依赖性。
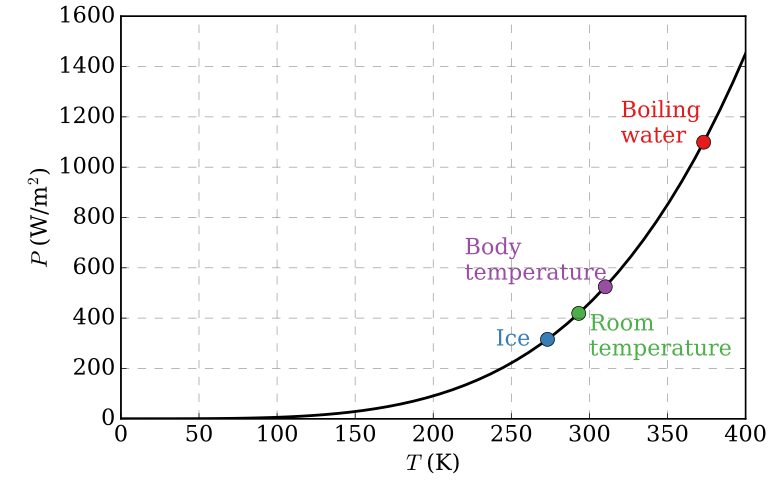
图 1.1.4 : 黑体总发射能量与其热力学温度的四次方成正比的函数图T根据 Stefan-Boltzmann 定律。 例 1.1.1太阳的表面温度为 5700 K。 l 太阳辐射多少功率? l 鉴于到地球的距离约为 200 个太阳半径,那么 1 平方公里太阳能装置的最大可能功率是多少?
解答(a) 首先,我们计算太阳的面积,然后计算磁通量(功率)。太阳的半径为6.96×108m 太阳的面积为A=4πR2. A=4(3.1416)(6.96×108m)2=6.08×1018m2
太阳辐射的功率(通过斯蒂芬-玻尔兹曼定律)为P=σT4(方程1.1.1). P=(5.67×10−8Wattsm−2K−4)(5700K)4=5.98×107Watts/m2 该值为每平方米。
(b) 计算太阳辐射的总功率是: Ptotal=PA=(5.98×107Watts/m2)(6.08×1018m2)=3.6×1026Watts
维恩位移定律实验的第二个现象学观察是维恩位移定律。维恩定律确定了在给定温度下来自物体的光的主(峰值)波长或颜色。随着烘箱温度的变化,发射辐射最强的频率也会变化(图 1.1.3 ).事实上,该频率与绝对温度成正比:
其中,比例常数为 5.879×1010Hz/K 1893 年,Wien 本人遵循玻尔兹曼的热力学推理,从理论上推导出了这条定律。它之前曾由美国天文学家兰利 (Langley) 观测到,至少是半定量的。这种向上的转变νmax跟T大家都熟悉的当熨斗在火中加热时(图 1.1.1 ),第一个可见辐射(大约 900 K)是深红色,这是频率最低的可见光。进一步增加TT导致颜色变为橙色,然后变为黄色,最后在非常高的温度(10,000 K 或更高)下变为蓝色,其中辐射强度的峰值已从可见光进入紫外线。 维恩定律的另一种表示形式(方程1.1.2) 根据光的峰值波长为
这里T是以开尔文为单位的绝对温度,b是一个称为 Wien 位移常数的比例常数,等于2.89×10−3mK,或者更方便地获得以微米为单位的波长,b≈2900μmK.这是波长和温度之间的反比关系。因此,温度越高,热辐射的波长越短或越小。温度越低,热辐射的波长越长或越大。对于可见光辐射,热物体发出的光比冷物体发出的光更蓝。
例 1.1.2l 如果体表温度为 90 °F。 l 辐射能在Wm−2你的身体会分泌吗? l 发射辐射的峰值波长是多少? l 您的身体发出的总辐射能(以瓦特为单位)是多少?注意:成年男性的平均体表面积约为 1.9m2女性的平均体表面积约为 1.6m2. 解答(a) 90 °F 等于 305 K。我们使用 Stefan-Boltzmann 定律(方程1.1.1).发射的辐射总量将为P=σT4. P=(5.67×10−8Wattsm−2K−4)(305K)4=491Wm−2
发射辐射的峰值波长使用维恩定律找到: λmax=2.898×10−3mK/T=2.898×10−3mK/305K=9.5×10−6m=9.5μm
以瓦特为单位的总辐射能密度为: Energymale=(491Wm−2)(1.9m2)=933W Energyfemale=(491Wm−2)(1.6m2)=786W 例 1.1.3 :太阳的温度例如,如果太阳的表面温度为 5700 K,那么太阳辐射的最大强度波长是多少? 解答如果我们将 5700 K 替换为T在方程中1.1.3我们有 λmax=0.0029/5700=5.1×10−7m 知道紫光的波长约为4.0×10−7m, 黄色约5.6×10−7m,红色约6.6×10−7m,我们能说太阳峰值辐射的颜色吗?太阳辐射的峰值波长比黄色的波长略短,因此呈略带绿黄色的波长。要看到太阳的这种绿色调,你必须从太空中观察它。事实证明,地球大气层会散射一些较短的太阳光波,从而将其峰值波长转变为纯黄色。 请记住,热辐射总是跨越很宽的波长范围(图 1.1.2 ) 和 Equation1.1.3仅指定作为光谱峰值的单个波长。因此,尽管太阳看起来是黄白色的,但当你用棱镜驱散阳光时,你会看到彩虹所有颜色的辐射。黄色仅表示发射的特征波长。
Rayleigh-Jeans 定律Lord Rayleigh 和 J. H. Jeans 开发了一个方程式来解释低频下的黑体辐射。这个似乎表达黑体辐射的方程式是建立在当时所有已知的物理学假设之上的。Rayleigh 和 Jean 暗示的一个大假设是,当频率增加时,无限小的能量会不断添加到系统中。经典物理学假设原子振荡发射的能量可以具有任何连续值。在那之前研究的任何东西都是如此,包括加速度、位置或能量等。他们得出的 Rayleigh-Jeans 定律是
在黑匣子上进行的实验数据显示的结果与 Rayleigh-Jeans 定律的预期略有不同(图 1.1.5 ).当时许多物理学家已经研究并广泛接受了该定律,但实验结果并没有说谎,理论上的和实际发生的事情之间存在一些差异。实验结果显示钟形曲线,但根据 Rayleigh-Jeans 定律,频率在接近紫外线区域时发散(方程1.1.5).Ehrenfest 后来将此称为“紫外线灾难”。重要的是要强调方程1.1.5是经典结果:唯一的输入是经典动力学和麦克斯韦电磁理论。
图 1.1.5 物体的温度与其发射的黑体辐射光谱之间的关系。在相对较低的温度下,大多数辐射以超过 700 nm 的波长发射,该波长位于光谱的红外部分。图 1.1.5 中热金属制品的暗红色光芒 是由于在小于 700 nm 的波长处发射的少量辐射,肉眼可以检测到。随着物体温度的升高,最大强度转移到更短的波长,依次产生橙色、黄色,最后产生白光。在高温下,所有波长的可见光都以大致相等的强度发射。 分布的微分与积分表示辐射被理解为振幅与波长的连续分布,或者等效地,振幅与频率的连续分布(图 1.1.5 ).根据 Rayleigh-Jeans 定律,特定频率下的强度νν且温度为
然而,在实践中,我们对频率间隔更感兴趣。精确频率是一系列越来越小的区间的极限。如果我们假设,在足够小的区间内,ρ(ν,T)不变,我们得到您对 Differential 的定义dρ(ν,T)在方程中1.1.5: 由于ρ(ν,T).这是在非常小的区间上积分的近似值dν乘以此区间内点的高度 (8πkbTν2/c3) 乘以其长度(dν).因此,如果我们对像上面这样的无限数量的小区间求和,我们会得到一个积分。之间的总辐射ν1和ν2将是:
请注意ρ(ν,T)在 中是二次的ν.
例 1.1.4 :紫外线灾难对于发射光谱,遵循 Rayleigh-Jeans 定律的发射器的总光谱辐射度是多少? 解答总光谱辐射度ρtot(T是所有可能波长(或等效于频率)的组合发射,它是相关分布的积分(方程1.1.5Rayleigh-Jeans 定律)。
但是
不会收敛。更糟糕的是,它是无限的,
因此,经典推导的 Rayleigh-Jeans 定律预测黑体的光芒是无限的。由于辐射度是每个角度和单位面积的功率,这也意味着黑体发射器发出的总功率和能量是无限的,这显然是荒谬的。这被称为紫外线灾难,因为荒谬的预测是由于经典定律没有正确预测高频/小波长的行为引起的(图 1.1.5 ).
Contributors and Attributionsl Michael Fowler (Beams Professor, Department of Physics, University of Virginia) l David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules") l Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd2-4908-8563-90b8a7ac8df6@9.110). l ACuriousMind (StackExchange) |