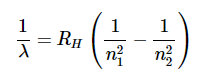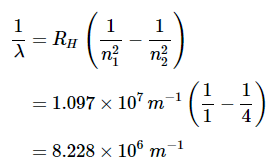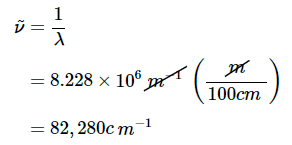1.5：里德伯公式和氢原子光谱

学习目标

l 描述一下Rydberg的氢光谱理论。

l 根据电子的能量状态解释氢谱。

1885年，Balmer提出了一个简单的公式，用于预测我们现在所知的Balmer级数中氢原子中任何线的波长，这是对数学洞察力的惊人演示。三年后，里德伯格将其推广化，以便可以确定氢发射光谱中任何一条线的波长。里德伯格认为，所有原子光谱都形成了具有这种模式的族（他不知道Balmer的工作）。事实证明，有遵循里德伯格模式的光谱族，特别是在碱金属、钠、钾等中，但氢原子线不符合Balmer公式的精度，并且n2预测的波长偏差很大。

里德伯格的现象学方程如下：

这里R_H是里德伯常数，等于109,737cm-1(2.18×10⁻¹⁸J）和n1和n2是整数（整数），其中n2>n1.

对于Balmer系列，n1=2和n2可以是3到无穷大之间的任何整数。可以代入该公式的各种数字组合允许计算氢发射光谱中任何线的波长;此公式生成的波长与在实际光谱中观察到的波长之间有密切的一致性。

其他系列

Balmer和Rydberg给出的电磁辐射可见区域光谱的结果以n2=3和n1=2.是否有具有以下公式的不同系列（例如，n1=1)?

n2的值和wavenumberν˜对于这个系列，将是：表1.5.1：Lyman系列氢发射线

您知道这些线位于电磁辐射的哪个区域吗？当然，这些线在UV区域，它们不可见，但它们会被仪器检测到;这些线形成莱曼级数。莱曼级数和巴尔默级数的存在表明存在更多的级数。例如，具有n1=3和n2=4,5,6,7，...被称为Paschen系列。

谱线根据n1值。线路从系列的最长波长/最低频率开始按顺序命名，在每个系列中使用希腊字母。例如，（n1=1/n2=2）行称为“Lyman-alpha”（Ly-α），而（n1=3/n2=7）线称为“Paschen-delta”（Pa-δ).前6个系列有特定名称：

l Lyman系列n1=1

l Balmer系列n1=2

l Paschen系列（或Bohr系列）n1=3

l Brackett系列n1=4

l Pfund系列与n1=5

l Humphreys级数n1=6

例1.5.1：Lyman系列

氢发射光谱中所谓的莱曼级数线对应于从各种激发态到n=1轨道的跃迁。将莱曼级数中能量最低的线的波长计算为三个有效数字。它发生在电磁波谱的哪个区域？

鉴于：莱曼级数中能量最低的轨道

要求：最低能量莱曼线的波长和光谱的相应区域

策略：将适当的值代入方程1.5.2（里德伯格方程）并求解λ.

找到与计算的波长相对应的电磁波谱区域。

解答

我们可以使用里德伯格方程（方程1.5.2）计算波长：

解决方案A

对于Lyman系列，n1=1

光谱学家经常将能量和频率等价。cm^-1unit（wavenumbers）特别方便。我们可以将A部分中的答案转换为cm^-1.

和

λ=1.215×10⁻⁷m=122nm

这条发射线被称为莱曼阿尔法，是来自太阳的最强原子发射线，它通过从原子和分子中剥离电子来驱动所有行星上层大气的化学反应，产生离子。它被平流层上部的氧气完全吸收，解离O2分子与其他O原子反应2形成平流层臭氧的分子

解决方案B

他的波长在光谱的紫外区域。

上述讨论仅提供了氢发射线的现象学描述，未能提供对原子本身性质的探测。显然，基于经典力学的连续介质模型并不适用，正如下一节所展示的，光谱和原子结构之间的简单联系是可以制定的。