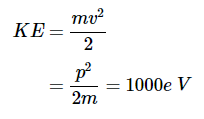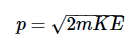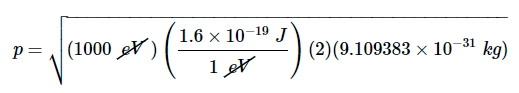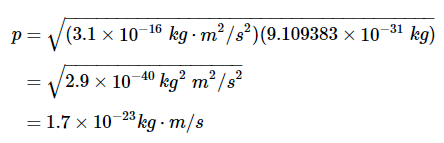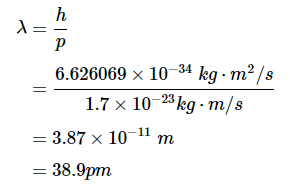1.6：物质具有波状特性

学习目标

l 介绍光的波粒二象性延伸到物质

l 描述物质（例如电子和质子）如何表现出波状特性，例如干涉和衍射图

l 使用代数求给定这些量中的任何一个时粒子的德布罗意波长或动量

理解原子的下一个真正进步来自一个不太可能的地区——巴黎的一位学生亲王。路易·德布罗意亲王（PrinceLouisdeBroglie）是一个显赫家族的成员，自1600年代以来在政治和军事领域享有盛誉。路易斯从历史开始了他的大学学习，但他的哥哥莫里斯在自己的实验室里研究X射线，路易斯对物理学产生了兴趣。第一次世界大战后，德布罗意将注意力集中在爱因斯坦的两项重大成就上，即狭义相对论和光波量子化。他想知道他们之间是否有某种联系。也许辐射的量子真的应该被认为是一个粒子。德布罗意建议，如果波（光子）可以表现为粒子，如光电效应所证明的那样，那么反之，即粒子可以表现为波，应该是正确的。他将一个波长λ转换为具有动量的粒子p使用普朗克常数作为比例常数：

这称为the de Broglie波长。粒子既可以表现为波，也可以表现为粒子，这取决于你对它们进行的实验，这一事实被称为波-粒二象性。

推导德布罗意波长

从光电效应的讨论中，我们得到了粒子波二象性的第一部分，即电磁波可以表现得像粒子。这些粒子被称为光子，它们以光速移动。任何以光速或接近光速运动的粒子都具有爱因斯坦的相对特理论给出的动能。通常，质量为m和动量有一种能量

请注意，如果p=0，这归结为著名的rest-energy表达式E=mc2.然而，光子是无质量的粒子（技术上是无静止质量的），它们总是具有有限的动量p.在本例中，方程1.6.2成为

E=pc.

根据普朗克的假设，一个量子电磁辐射具有能量E=h..因此，将这两个表达式等同于光子的动能，我们得到

求解波长λ给出方程1.6.1:

λ=h/p=h/mv

这里v是粒子的速度。因此，德布罗意认为，如果粒子可以表现为波，那么像这样的关系，特别是与波有关的关系，也应该适用于粒子。

方程1.6.1允许我们关联一个波长λ转换为具有动量的粒子p∙As动量增加，波长减小。在这两种情况下，这意味着能量变得更大。即，短波长和高动量对应于高能量。

量子力学的一个共同特征是，短波长的粒子和波对应于高能量，反之亦然。

在确定光子很可能是一个具有静止质量的粒子后，即使非常小，德布罗意突然意识到，在其他方面，它可能与其他粒子没有太大区别，尤其是非常轻的电子。特别是，也许电子也有一个相关的波。明显的反对意见是，如果电子是波状的，为什么没有观察到衍射或干涉效应？但有一个答案。如果德布罗意的动量和波长之间的关系也适用于电子，那么波长足够短，以至于很容易错过这些效应。正如德布罗意自己所指出的，光的波动性质在日常生活中并不是很明显。正如下一节将要展示的那样，1926年G.P.Thomson和C.Davisson和L.H.Germer在1927年的电子衍射实验证实了deBroglie提议的有效性。在这些实验中，发现电子从晶体中的原子散射，并且这些散射的电子产生了干涉图样。这些衍射图案是波状行为的特征，由电子（即物质）和电磁辐射（即光）表现出来。

例1.6.1：电子波

计算动能为1000eV的电子的德布罗意波长。

解答

要计算德布罗意波长（方程1.6.1），必须确定粒子的动量，并且需要了解粒子的质量和速度。电子的质量为9.109383×10⁻²⁸g速度由给定的1000eV动能获得：

求解动量

转换为SI单位

将焦耳的定义扩展为基本SI单位并取消

现在将动量代入德布罗意波长的方程中（方程1.6.1）替换为普朗克常数（h=6.626069×10⁻³⁴J∙s).展开普朗克常数中的单位后

这是亲王于1924年提交的博士论文。他的论文导师有些吃惊，不确定这是否是合理的工作。他向德布罗意索要了一份额外的论文副本，并寄给了爱因斯坦。爱因斯坦不久后写道：“我相信这是我们这个最糟糕的物理学谜团的第一道微弱曙光”，亲王获得了博士学位。