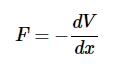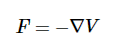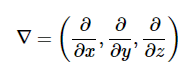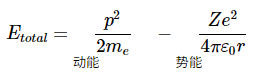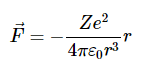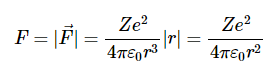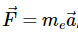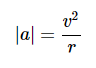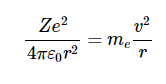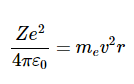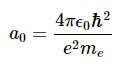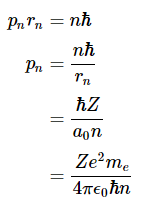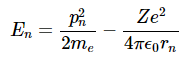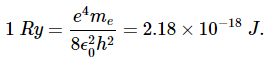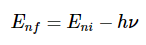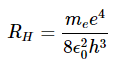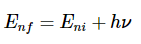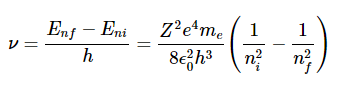1.8：氢原子的玻尔理论

学习目标

介绍玻尔原子背后的基本原理，并证明它可以预测氢原子谱的里德伯方程

卢瑟福的失败行星原子

欧内斯特·卢瑟福（ErnestRutherford）提出了一个基于α-HansGeiger和ErnestMarsden的粒子散射实验。在这些实验中，氦原子核（α-粒子）被射向薄金金属箔。大多数颗粒没有分散;它们原封不动地穿过薄薄的金属箔。少数分散的人中，有的分散在后面;也就是说，他们退缩了。这种向后散射要求箔片包含重颗粒。当α粒子击中其中一个重粒子时，它只会向后反弹，就像向砖墙扔球一样。由于大多数α粒子不会分散，重粒子（原子核）必须只占据原子总空间的非常小的区域。大部分空间必须是空的或被质量非常低的粒子占据。这些低质量粒子是围绕原子核的电子。

卢瑟福模型存在一些基本问题。存在于带相反电荷的粒子之间的库仑力意味着正原子核和负电子应该相互吸引，原子应该坍缩。为了防止坍缩，假设电子围绕正原子核运行。库仑力（下面讨论）用于改变速度的方向，就像一根绳子在绕你头的圆形轨道上拉球，或者引力将月球保持在环绕地球的轨道上一样。这个假设表明这种观点是合理的，其起源是引力和库仑相互作用的相似性。两个质量之间的引力表达式（牛顿万有引力定律）为

m1和m2分别表示物体1和2的质量，而r表示对象中心之间的距离

两种带电物质之间的库仑力表达式为

Q1和Q2分别代表物体1和2的电荷，以及r表示对象中心之间的距离。

然而，这个类比也有问题。一个在圆圈中旋转的电子不断被加速，因为它的速度矢量正在变化。正在加速的带电粒子会发出辐射。此属性实质上是无线电发射器的工作原理。电源驱动电子在电线上上下移动，从而传输无线电接收器接收到的能量（电磁辐射）。然后收音机为您播放编码在辐射能量波形中的音乐。

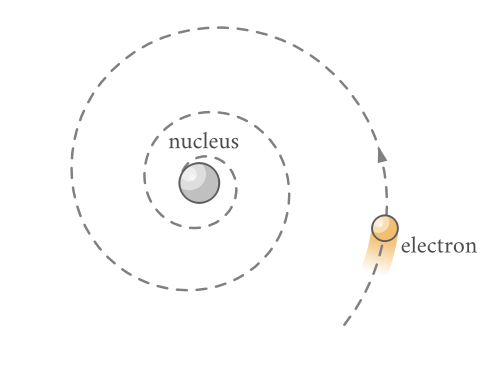
图1.8.1：电子围绕原子核的经典死亡螺旋。

如果轨道电子产生辐射，它就会失去能量。如果轨道上的粒子失去能量，则轨道的半径会减小。为了保持角动量，绕轨道电子的频率增加。当电子向原子核坍缩时，频率不断增加。由于旋转电子的频率和发射的辐射频率相同，因此两者都会不断变化以产生连续的光谱，而不是观察到的离散线。此外，如果计算这种崩溃发生需要多长时间，就会发现它大约需要10^-11秒。这意味着世界上没有任何东西可以存在超过大约10⁻¹¹秒。显然，这幅经典图景存在严重问题，这意味着当时已知的物理定律中缺少一些东西。

保守力可以用势能来解释

保守力仅取决于物体的位置。如果力是保守的，则可以为任何点的电位分配一个数值。当物体从一个位置移动到另一个位置时，力会改变物体的势能，其变化量不取决于所采用的路径。势能可以构造为一维力的简单导数：

或作为3-D力的梯度

哪里∇是偏导数的向量

最熟悉的保守力是引力和库仑力。

库仑力定律（方程1.8.2）来自相应的库仑电势（有时称为静电电势）

并且可以很容易地验证来自这种相互作用的库仑力（F(r)）是

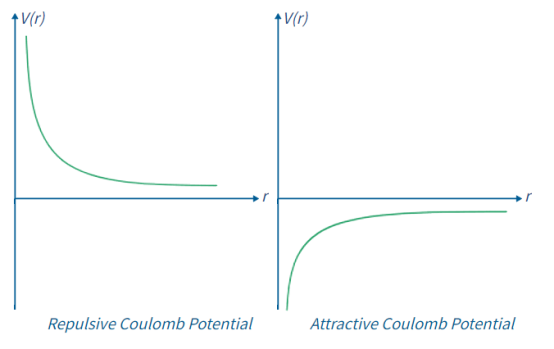
如r是变化的，能量会发生变化，所以我们有一个势能曲线的例子V(r)（图1.8.2左)。如果Q1和Q2是相同的符号，那么曲线是纯粹的排斥势，即能量随着电荷的聚集而单调增加，当它们分离时能量单调减少。由此，很容易看出likecharges（相同星座的电荷）相互排斥。

图1.8.2：相同符号（左）和相反符号（右）的两个电荷之间的库仑相互作用的势能曲线。

如果电荷的符号相反，则曲线大致显示图1.8.2;右这纯粹是一个有吸引力的势能。因此，能量随着电荷聚集在一起而减少，这意味着相反的电荷吸引。

玻尔模型

据观察，前几节中讨论的线光谱表明，氢原子仅吸收和发射离散波长的光。这一观察结果与量子力学系统允许能量的离散性质有关。量子力学假设，与经典力学相反，系统的能量只能具有某些离散值。这给我们留下了一个问题：我们如何确定这些允许的离散能量值是多少？毕竟，普朗克的允许能量公式似乎是凭空出现的。

由于NielsBohr在1913年提出的，我们在这里描述的模型是预测单电子原子允许能量的早期尝试，例如H,He⁺,Li²⁺,Be³⁺,等。尽管玻尔的推理依赖于古典概念，因此不是一个正确的解释，但推理很有趣，因此我们研究了这个模型的历史意义。

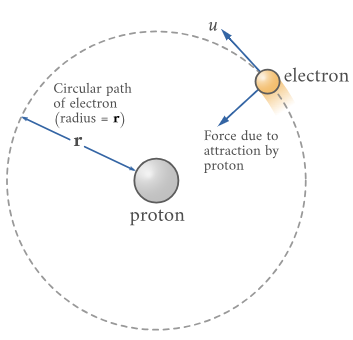
图1.8.3：具有围绕固定原子核旋转的电子的玻尔原子。

考虑一个带电荷的原子核+Ze和一个围绕原子核运行的电子。在此分析中，我们将使用常数的另一种表示形式k在库仑定律中（方程1.8.3），它更常见的表示形式为：

这里ε0称为自由空间的介电常数，其数值为ε0=8.8541878×10⁻¹²C²J⁻¹m⁻¹

电子的总能量（假设原子核在原点的空间中固定）是动能和势能之和：

电子上的力是

其大小为

因为

所以大小为

.如果我们假设轨道是圆形的，那么加速度是纯粹的向心的，所以

这里v是电子的速度。力|F|等于m_e|a|，我们获得

或

或

以这种方式写方程的原因是m_evr是电子的经典轨道角动量。玻尔熟悉麦克斯韦的经典电磁理论，并且知道在经典理论中，轨道上的电子应该将能量辐射出去并最终坍缩到原子核中（图1.8.1）。他通过遵循普朗克的黑体辐射思想来规避这个问题，并假设轨道角动量m_evr的电子只能取特定的值

其中n=1,2,3，...

请注意，电子必须处于运动状态，因此n=0是不允许的。

替换方程1.8.7代入到（方程式）1.8.6，我们发现

方程1.8.8意味着轨道只能具有一定的允许半径

其中n=1,2,3，....常量集合被定义为a0

这个量称为玻尔半径。

我们还可以计算允许的动量，因为m_evr=nħ和p=mev.因此

其中p_n和r_n，我们可以根据

将表达式替换为p_n和r_n而简化得到

我们可以通过将里德伯格定义为

这简化了玻尔模型预测的允许能量（方程1.8.11）设置为

因此，原子中电子的能量也被量子化。方程1.8.12给出氢原子的电子状态的能量。在分析光谱时，在能级图中以图形方式表示这些能量非常有用。能级图在纵轴上绘制了能量，并绘制了一条水平线来定位每个能级（图1.8.4）。

图1.8.4：氢的玻尔模型预测的能级（Z=1).

这些被证明是正确的能级，除了在这种伪经典处理中无法解释的小修正。尽管能量基本上是正确的，但玻尔模型掩盖了电子的真正量子性质，它只能从完全量子力学分析中出现。

量化的Wave参数

上述讨论基于轨道电子的经典图片，其中角动量进行了量子化（方程1.8.7）要求从Planck的量化参数中提升。因此，只允许某些轨迹是稳定的（具有不同的半径）。然而，如前所述，电子也将具有德布罗意波长的波状特性λ

λ=h/p

因此，动量p更大意味着波长更短。这意味着n增加（公式1.8.12)，波长也必须增加；这是量子力学中的一个共同特征，经常被观察到。在玻尔原子中，电子的圆周对称性和波特性要求电子波具有整数个波长（图一个1.8.1).否则，波将不完全重叠并抵消（即，电子将不复存在），如图1.8.1B

图1.8.5：弦上的波具有与弦长度相关的波长，允许它们进行建设性干涉。（A）如果我们想象弦弯曲成一个闭合的圆圈，我们就会大致了解圆形轨道中的电子如何建设性地干涉。（B）如果波长不适合圆周，则电子会发生破坏性干涉;它不能存在于这样的轨道上。

以下章节将更详细地讨论电子波对原子的影响。

从玻尔模型推导里德伯方程

给定对系统允许能量的预测，我们如何验证它们呢？被称为光谱学的一般实验技术允许我们探测允许的能量之间的各种差异。因此，如果实际能量本身的预测是正确的，我们也应该能够预测这些差异。假设我们能够将玻尔氢原子中的电子置于能量状态En，对于n>1即，其中一个所谓的激发态。电子会迅速回到其最低能量状态，即基态，并在此过程中发射光。光携带的能量由总能量守恒的条件决定（图1.8.6 )。

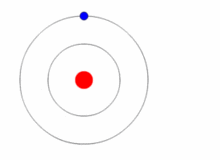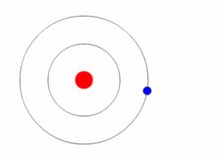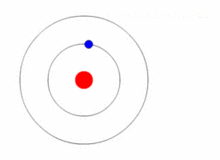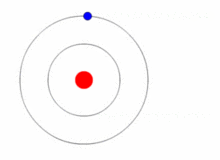
图1.8.6玻尔原子模型的简单插图，电子进行量子跳跃。

因此，如果ni是描述电子的初始（激发）状态的整数，并且nf最终状态（这里我们想象nf=1，但适用于以下情况nf<ni，即发射）

或

我们现在可以确定里德伯常数R_H

其中Equation右侧的常数比1.8.13

评估R_H从这个公式的基本常数得出的值与从氢原子光谱中实验得到的值相差不到0.5%。

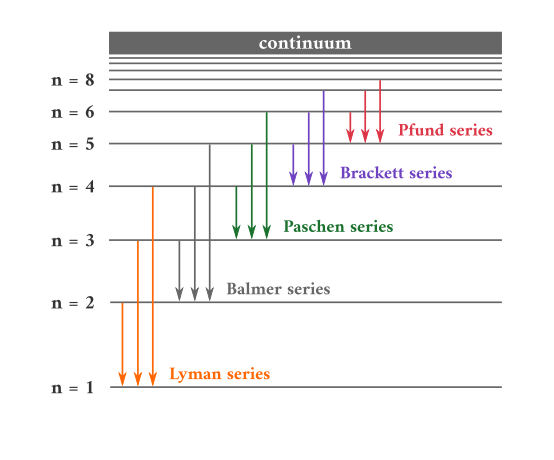
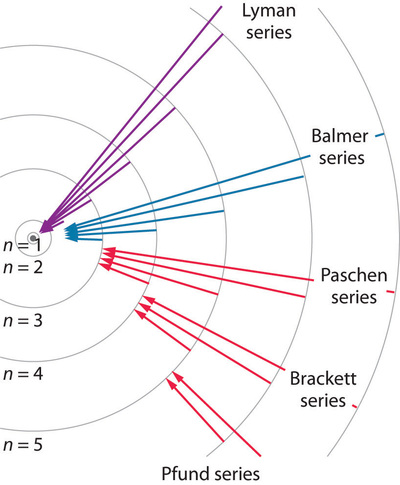
因此，通过观察发射光，我们可以确定初始能级和最终能级之间的能量差，这导致了第1.4节和第1.5节中讨论的发射光谱。不同的nf值决定观测到的发射光谱，并且图中所示的例子以首次观测到它们的个人命名。下图显示了不同nf和ni可能的一些跃迁。

图1.8.7：负责在氢发射光谱中观察到的各种系列线的电子跃迁。莱曼级数线是由于从高能轨道到最低能轨道（n=1）的转变;这些跃迁释放出大量能量，对应于电磁波谱中紫外线部分的辐射。Paschen、Brackett和Pfund系列线是由于从高能轨道到n=3、4和5的轨道的转变;这些跃迁释放的能量比红外辐射少得多。轨道不是按比例绘制的。

如果原子吸收了光，它最终会因为吸收而进入激发态。这种吸收仅对特定频率的光是可能的，再次强调，能量守恒决定了这些频率是多少。如果光被吸收，其中当nf>ni那么最终的能量Enf将与初始能量Eni相关，通过

或

玻尔的提案解释了氢原子光谱、里德伯公式的起源以及里德伯常数的值。具体来说，它证明了Rydberg公式中的整数是量化的一种表现形式。能量、角动量和轨道电子的半径都是量子化的。这种量子化也与Bohr模型中的稳定轨道概念相似。只有E,M和r是可能的，因此电子不能通过持续辐射能量坍缩到原子核上，因为它只能具有一定的能量，而不能位于空间的某些区域。电子只能从一个轨道（量子态）跳到另一个轨道。量子化意味着轨道是稳定的，尽管有吸引的库仑力，但电子不能螺旋进入原子核。

尽管玻尔的想法成功地解释了氢光谱，但在应用于其他原子的光谱时却失败了。此外，还有一个深刻的问题。为什么角动量以ħ?正如我们将看到的，德布罗意对这个问题有答案，这个答案使薛定谔得出了一个一般假设，该假设因此产生了角动量的量子化。这种量子化并不像Bohr提出的那么简单，我们将看到不可能像Bohr认为的那样精确地确定电子与原子核的距离。事实上，由于电子在氢原子中的位置根本不像经典轨道（例如月球绕地球运行）那样定义，因此它被称为轨道。电子轨道用称为波函数的数学函数来表示或描述电子围绕原子核的位置，该函数产生电子位置的概率。

Contributors and Attributions

l Mark Tuckerman (New York University)

l David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")

l Template:Contriboundless