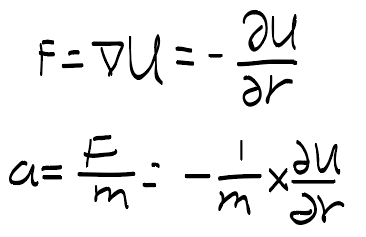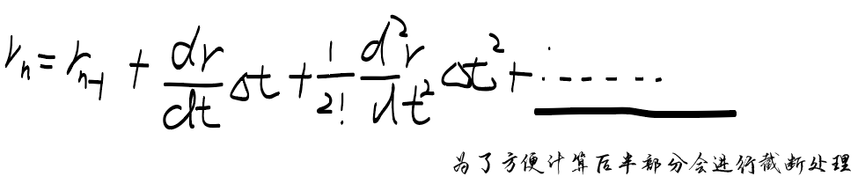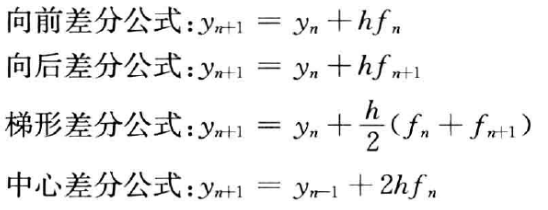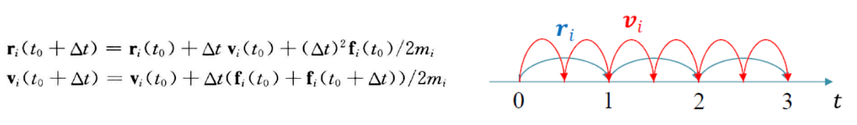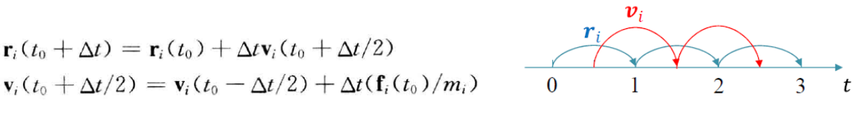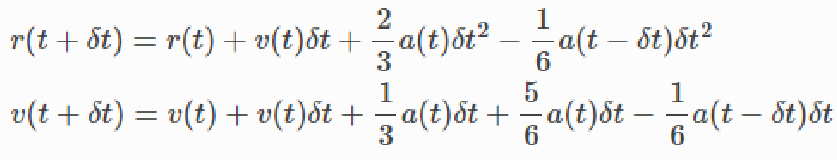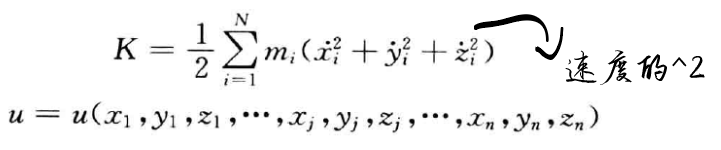|
如何求解运动方程时间:2025-05-21 求解牛顿方程是分子动力学的核心,之前讲了F=ma,那么推导出 对于势能的求导,力就是势能的梯度 速度是位移的一阶导数 加速度是二阶导数 里面需要进行泰勒展开进行求解
U是势能,由分子力场进行定义,m是质量确认,所以上述关联只有r(t)与v(t) 关于t的取值,由于电脑计算是根据取点进行计算,不可能是直接画出连续的曲线 所以t的点应该是离散型的,那么对于tn=n*步长,因为t0=0,tn就等与n个步长 t可以进行设定,那么这个时候我们重点是需要求出位置 r~(r0,t),这个时候用泰勒展开式进行处理
求解这个牛顿方程,可以直接用差分公式进行求解
这个就是最早的Verlet算法的思路
由于Verlet算法的局限性,所以延伸出2种比较好的方法 一种VV算法(速度Verlet算法)
速度与坐标可以同时得到,相对更加精准 一种Leap-frog法(蛙跳法)
相对Verlet算法更好,但是没法同时得到两个值,导致在控温时存在一定的影响 速度 verlet 不适用于有粘性(速度)影响加速度(力)的 CFD 问题, 可用于不受速度影响加速度(力)的分子动力学问题; 蛙跳法虽然采用半步长相互迭代的处理思路, 但处理会使本方法在实际操作时的近似处理影响计算精度, 精度可能会在理论精度附近抖动,略低于理论精度(截断的局部误差) Beeman’s算法:基于Verlet算法改进体系的粒子位置和速度分别为,
Beeman’s算法的计算精确度得到了极大的提高,但计算成本也相应提高 除了求解牛顿方程还有一种就是关于哈密顿运动方程进行求解 其原理为H=K+U,K为动能,U为势能 原子受到的力是一种保守力,就是说他们做的功位置无关 由于K与位置无关,并且U与位置有关与t没有关系
采用内坐标的方法进行处理,采用分析相空间的方法 相比于求解牛顿方程来说 牛顿方程需要计算3N个二阶微分方程 哈密顿需要计算2(3n-r)个一阶微分方程,r为约束个数 对于没有约束条件下的计算其实是等价的 对于有约束条件下,两者的形式不同 |