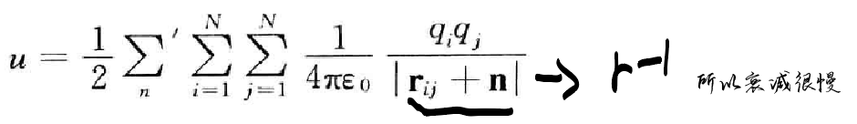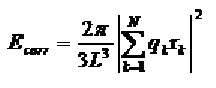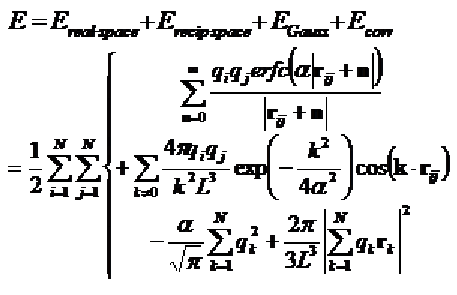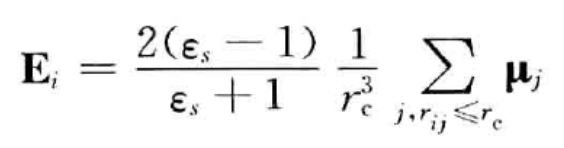库伦作用计算

长程作用通常是指相互作用力随着粒子之间的距离而衰减得很慢的相互作用

而短程作用是指相互作用力在一定截断半径范围内迅速衰减

库伦作用属于长程势，不能用之前计算范德华作用的方法进行处理

这个时候你是需要考虑他的镜像中的粒子进行计算的

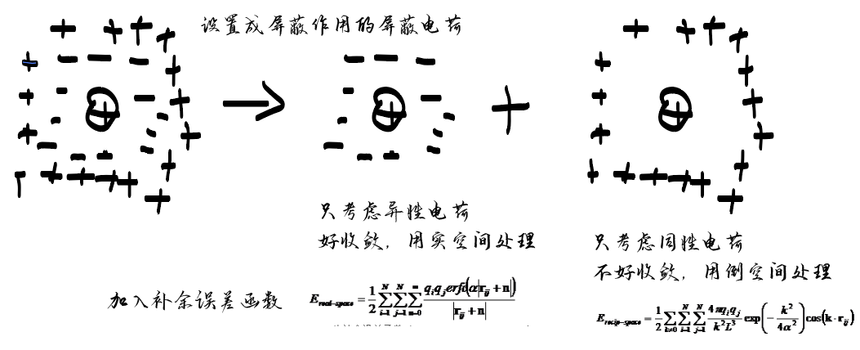
如果你是考虑孤立体系就把cutoff设置较大

如果你考虑的是周期性体系，则需要考虑上面的n作为周期性的影响

因为要考虑镜像所以需要的计算方法来进行处理

否则计算的话会比较麻烦

所以计算库伦作用的核心就是处理如何快速收敛的相关计算

目前常用的处理方法：Ewald方法

因为前面的公式比较难收敛，收敛的很慢，就是需要计算大量的数值之后才能缩小误差

通常的做法是，把它分解成收敛比较快的两项

就是将相互作用势分为短程力和无奇点的长程力两部分，

短程力在实空间中好求，长程力放入倒空间进行求解，就是将边长成为倒数

这样就容易方便进行做收敛处理，所以长程力用傅里叶变换计算，会用到高斯型函数表示

在实空间部分的计算中，会引入截断半径来限制相互作用的计算范围

然而，由于截断操作会导致计算的不完全，会引入一定的误差

计算库伦作用中还需要考虑的2个计算量分别为

3需要扣除每个Gaussian函数之间的自相互作用

α需要注意，他越大实际空间更好处理，但是倒空间就麻烦

所以需要讲究平衡性，一般程序不让调整的

4静电相互作用能量形式是环绕模拟盒子周围的介质和球形盒子之间的校正项

总的表达式是这个

在Ewald加和法中加入快速傅立叶转换方法

需要用基于网格分布的电荷取代连续坐标下的点电荷

此时每个原子的电荷要处理成分布在其周围的网格点上

这样在原始点周围就会产生电势

周围划分的网格点越多

计算的结果越准确，计算量也会越大

Ewald方法虽然是比较好用的方法，但是其计算量依然非常大，

可以借鉴前面说的网格索引法进行处理particle-mesh method

在三维空间上考虑最近的27个格子点

通过这种格子电荷密度，利用快速傅立叶转换方法计算每个格子点上的电势

随后再转化到作用在每个粒子上的势（或者力）

但是这种方法其准确性相对较低，尤其对于相互作用有强烈波动的系统

因此现在常用的方法有PME

它是采用3D FFT（三维快速傅里叶变换）使得倒空间更好计算，提高效率

它的原理是将电荷打散，然后通过配分函数进行分布到网格上

当然还有2种方法SPME和PPPM方法，精度应该差不多，具体的我也不懂

查看资料全部是公式，卧槽，需要的自己去看书

3D快速傅里叶变换（FFT）是一种高效的算法

可以将傅里叶变换的计算复杂度从O(n^2)降低到O(nlogn),其中n是数据点数目

3D FFT是在此基础上对三维数据做傅里叶变换的扩展

它利用了横向、纵向和垂直方向上的数据结构和对称性

以及一维FFT的计算优势来加速计算过程

一种在全原子不常见的方法叫做反应场的方法（在粗粒化计算中常用），了解就好

很多书都提了，我也顺便说下

这个原子在截断半径内的都进行计算

半径外的全部用恒定的介电常数来处理

半径内的也是用介电常数来处理

半径内的数目会经常发生变化

导致计算后的数据不连续

介电常数需要提前知道很麻烦

但是效果就是计算的速度更快