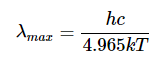1.2： 用于黑体辐射定律的量子假说

学习目标

了解黑体辐射中的能量是如何量化的

到 19 世纪后期，许多物理学家认为他们的学科正在解释大多数自然现象。他们可以使用牛顿经典力学定律计算物质物体的运动，他们可以使用称为麦克斯韦方程组的数学关系来描述辐射能的性质，该方程组由苏格兰物理学家詹姆斯·克拉克·麦克斯韦 （James Clerk Maxwell） 于 1873 年开发。宇宙似乎是一个简单而有序的地方，包含物质，它由有质量的粒子组成，其位置和运动可以准确描述，以及电磁辐射，它被认为没有质量，其在太空中的确切位置无法固定。因此，物质和能量被认为是不同且不相关的现象。然而，很快，科学家们开始更仔细地研究一些无法用当时可用的理论来解释的不便现象。

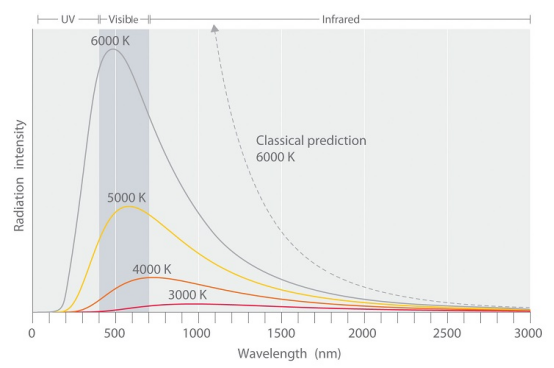
经典物理学无法充分解释的一种实验现象是黑体辐射（图 1.2.1 ).试图从经典理论中解释或计算这种光谱分布的尝试是完全失败的。Rayleigh 和 Jeans 提出的一个理论预测，在短波长下，强度应该达到无穷大。由于强度实际上在短波长下下降到零，因此 Rayleigh-Jeans 结果被称为紫外线灾难（图 1.2.1 虚线）。在黑体光谱的紫外区域，理论与实验之间没有一致性。

图 1.2.1 物体的温度与其发射的黑体辐射光谱之间的关系。在相对较低的温度下，大多数辐射以超过 700 nm 的波长发射，该波长位于光谱的红外部分。随着物体温度的升高，最大强度转移到更短的波长，依次产生橙色、黄色，最后产生白光。在高温下，所有波长的可见光都以大致相等的强度发射。物体在 6000 K 下显示的白光谱与太阳发出的光谱非常接近。请注意，在低于 400 nm 的波长下发射的辐射强度急剧下降，这构成了紫外线灾难。经典预测无法完全拟合实验曲线，并且没有最大强度。

量化

尽管量化似乎是一个陌生的概念，但我们在量子力学中经常遇到它（因此得名）。例如，美国货币是便士的整数倍。同样，钢琴或小号等乐器只能产生某些音符，例如 C 或 F 升号。由于这些仪器无法产生连续的频率范围，因此它们的频率被量化。它也类似于使用离散的楼梯台阶上下山坡，而不是能够在连续的斜坡上上下移动。当您从一个步骤移动到另一个步骤时，您的势能会呈现离散值。甚至电荷也被量化：离子的电荷可能为 -1 或 -2，但不是 -1.33 的电子电荷。

连续势能系统与量子化（引力）势能系统。在连续情况下（左），系统可以具有任何势能，但在量化情况下（右），系统只能具有某些值（不允许使用其他值）。

普朗克的能量量子化由他的著名方程式描述：

其中，比例常数h被称为普朗克常数，是科学中最准确已知的基本常数之一

h=6.626070040(81)×10⁻³⁴J∙s

但是，就我们的目的而言，它的值为四个有效数字就足够了：

h=6.626×10⁻³⁴J∙s

随着电磁辐射频率的增加，辐射能量的相关量子的大小也会增加。通过假设一个物体只能以的整数倍数发射能量hν，Planck设计了一个方程，该方程与图1.2.1中所示的实验数据拟合.我们可以定性地理解普朗克对紫外线灾难的解释如下：在低温下，仅发射频率相对较低的辐射，对应于低能量子。随着物体温度的升高，发射更高频率的辐射的可能性增加，对应于更高能量的量子。然而，在任何温度下，物体通过发射大量低能量量子而损失能量的可能性都大于对应于紫外线辐射的单个非常高能量的量子。结果是发射辐射强度与波长关系图中的最大值，如图1.2.1所示，以及随着温度的升高，最长到较低波长（较高频率）的位置发生变化。

在他提出他的激进假设时，普朗克无法解释为什么能量应该被量子化。最初，他的假设只解释了一组实验数据——黑体辐射。如果观察到大量不同现象的量化，那么量化将成为一种定律。随着时间的推移，可能会发展出一种理论来解释该定律。事实证明，普朗克的假说是现代物理学生长的种子。

马克斯·普朗克解释了电子振荡导致的黑体辐射的光谱分布。同样，天线中电子的振荡会产生无线电波。MaxPlanck专注于模拟烤箱壁中必须存在的振荡电荷，向内辐射热量，并且在热力学平衡中，它们本身由辐射场驱动。他发现，如果他要求这些振荡器不像经典理论所要求的那样连续辐射能量，他就可以解释观察到的曲线，但它们只能以块状的能量损失或获得能量，称为量子大小hν，对于频率为ν（方程1.2.1）

根据该假设，Planck发射器计算了以下炉内辐射能量密度的公式：

其中

π=3.14159

h=6.626×10⁻³⁴J∙s

c=3.00×10⁸m/s

ν=1/s

k_B=1.38×10⁻²³J/K

T是绝对温度（以开尔文为单位）

普朗克辐射能量密度（方程1.2.3）也可以用波长表示λ

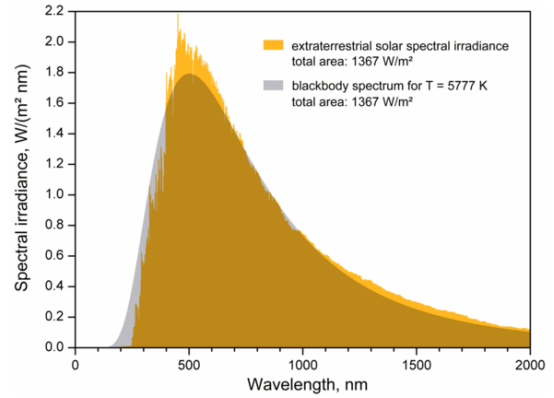
最大能量密度波长为：

普朗克方程（方程1.2.4）与所有温度下的实验观察结果极好一致（图1.2.2).

图1.2.2：太阳是黑体的极好近似值。其有效温度为~5777K.

该公式与精确实验（例如，图1.2.3）以及随之而来的能量量子化的必要性，是本世纪物理学中最重要的进步。他的黑体曲线被完全接受为正确的曲线：越来越准确的实验一次又一次地证实了这一点，但量子假设的激进性质并没有被理解。普朗克并没有太难过——他也不相信，他认为这是一种技术修复，（他希望）最终被证明是不必要的。

部分问题在于普朗克通往公式的道路漫长、困难且难以置信——正如爱因斯坦后来指出的那样，他甚至在不同阶段做出了相互矛盾的假设。然而，无论如何，结果是正确的！

数学表明，黑体发出的能量不是连续的，而是以某些特定波长以规则的增量释放。如果普朗克假设黑体辐射的能量是

E=nhν

这里n是一个整数，那么他可以解释数学所代表的含义。这对普朗克来说确实很难接受，因为在当时，没有理由假设能量应该只在特定频率上辐射。麦克斯韦定律中没有任何内容表明这样的事情。就好像弹簧末端的质量振动只能在特定能量下发生。想象一下，由于摩擦，质量会慢慢停止，但不是连续的。相反，质量从一个固定数量的能量跃升到另一个固定数量的能量，而不通过中间能量。

用一个不同的比喻来说，就好像我们一直想象的光滑的斜面实际上是一系列紧密间隔的台阶，只呈现出连续性的错觉。

总结

普朗克理论与实验观察之间的一致性提供了强有力的证据，证明物质中电子运动的能量是量子化的。在接下来的两节中，我们将看到光携带的能量也以hν.这些能量包称为“光子”。

ContributorsandAttributions

l MichaelFowler(BeamsProfessor,DepartmentofPhysics,UniversityofVirginia)

l DavidM.Hanson,EricaHarvey,RobertSweeney,TheresaJuliaZielinski("QuantumStatesofAtomsandMolecules")