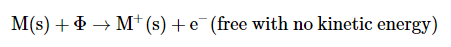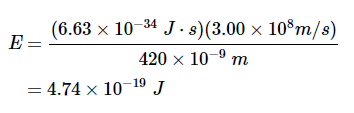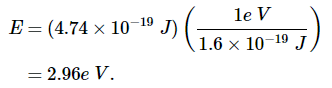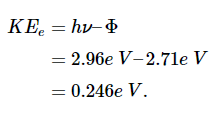1.3：用量子假说解释光电效应

学习目标

l 熟悉块状材料的光电子效应

l 了解光电子动能和强度如何随入射光波长的变化而变化

l 了解光电子动能和强度如何随入射光强度的变化而变化

l 描述什么是功函数并将其与电离能联系起来

l 用爱因斯坦的量子化光子模型描述光电效应

自然界似乎被量化了（非连续或离散）。如果是这样，麦克斯韦方程组如何正确预测黑体辐射器的结果呢？普朗克花了大量时间试图调和电磁波的行为与黑体辐射的离散性质，但无济于事。直到1905年，阿尔伯特·爱因斯坦（AlbertEinstein）发表了另一篇论文，光的波动性才被扩展到包括光的粒子解释，这充分解释了普朗克方程。

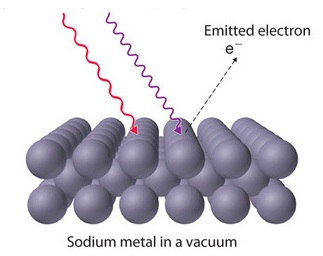
光电效应于1887年由德国物理学家海因里希·赫兹（HeinrichHertz）首次记录，因此有时被称为赫兹效应。在使用火花隙发射器（一种原始的无线电广播设备）时，赫兹发现，在吸收某些频率的光时，物质会发出可见的火花。1899年，J.J.Thomson将这种火花鉴定为离开金属表面的光激发电子（称为光电子）（图1.3.1).

图1.3.1：光电效应涉及用足够高能量的光子照射金属表面，使电子从金属中射出。

光电子效应背后的经典图景是金属中的原子包含电子，这些电子被入射辐射的振荡电场摇晃并引起振动。最终，它们中的一些会被摇松，并从阴极中弹出。值得仔细考虑发射的电子的数量和速度如何随入射辐射的强度和颜色以及观察光电子所需的时间而变化。

增加辐射强度会更剧烈地摇晃电子，因此人们会预期会发射更多，并且平均而言，它们会以更快的速度射出。

增加辐射的频率会更快地摇晃电子，因此可能会导致电子更快地出来。对于非常暗的光线，电子需要一些时间才能达到足够的振动幅度以松动。

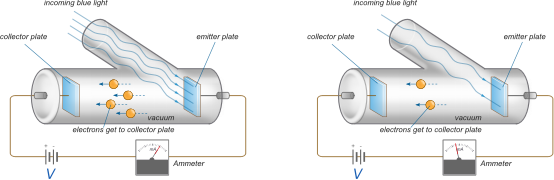
Lenard实验结果（强度依赖性）

1902年，赫兹的学生菲利普·莱纳德（PhilippLenard）研究了发射的光电子的能量如何随光的强度而变化。他使用了碳弧光，可以将强度提高一千倍。射出的电子撞击另一块金属板，即集电极，该金属板通过一根带有灵敏电流表的电线连接到阴极，以测量照明产生的电流（图1.3.2).为了测量射出的电子的能量，Lenard对集电极板进行负电荷，以排斥向它的电子。因此，只有以足够的动能射出的电子才能爬上这座势山，才能产生电流。

图1.3.2：莱纳德的光电实验。（左）高光强度会增加光电流（收集的光电子数）。（右）低光强度降低了光电流。然而，射出电子的动能与入射光强度无关。

Lenard发现有一个明确定义的最小电压可以阻止任何电子通过（V_stop).令莱纳德惊讶的是，他发现V_stop完全不取决于光线的强度！光强度加倍会使发射的电子数量增加一倍，但不会影响发射电子的动能。更强大的振荡场射出更多的电子，但射出的电子的最大单能与较弱的场相同（图1.3.2).

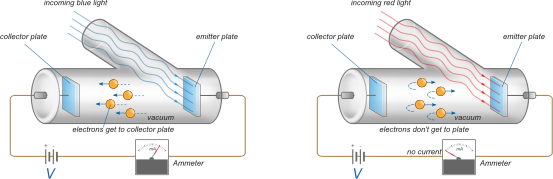
Millikan的实验结果（波长依赖性）

美国实验物理学家罗伯特·米利坎（RobertMillikan）跟进了莱纳德的实验，并使用强大的弧光灯，他能够产生足够的光强度来分离颜色并使用不同颜色的光检查光电效应。他发现射出的电子的最大能量确实取决于颜色——波长较短、频率较高的光射出的光电子具有更大的动能（图1.3.3).

图1.3.3：Millikan的光电实验。（左）入射高能蓝光。电池代表Lenard用于对集电板进行负电荷的电位，这实际上是一个可变电压源。由于蓝光射出的电子会到达集电极板，因此电池提供的电位小于V_stop，用于蓝光。（右）低能量红光。由于红光射出的电子没有到达集电极板，因此电池提供的电位超过V_stop用于红光。

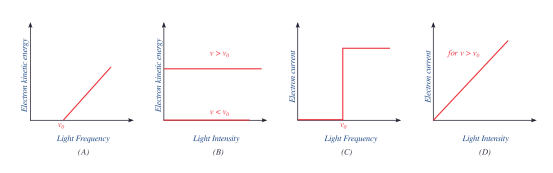
如图1.3.4所示，从Lenard和Millikan的实验中观察到与古典相反的行为。强度影响电子的数量，频率影响发射电子的动能。从这些草图中，我们看到

电子的动能与超过阈值ν0（下面没有观察到电流ν0），动能与辐射强度无关，并且电子数（即电流）与强度成正比，并且与高于阈值ν0（即，在下面没有观察到电流ν0).

图1.3.4：显示Lenard和Millikan实验中光电效应特性的示意图。（A）任何单个发射电子的动能随频率高于某个阈值而线性增加（B）电子动能与高于阈值频率和低于零的光强度无关。（C）每秒发射的电子数（即电流）与高于阈值频率的光频率和低于阈值频率的零无关。（D）电子数随光强度线性增加。

经典理论不描述实验

经典理论预测，光携带的能量与其振幅成正比，与其频率无关，这无法正确解释Lenard和Millikan观测中观察到的波长依赖性。

与我们在本文中讨论的大多数实验结果一样，上述行为是在实验室中观察到的真实实验结果的简化。更复杂的描述涉及对更复杂的物理和仪器的更多介绍，暂时将忽略。

爱因斯坦的量子图片

1905年，爱因斯坦对Lenard的结果进行了非常简单的解释，并从他的黑体研究中借用了普朗克关于量子化能量的假设，并假设入射辐射应被视为能量的量子hν跟ν频率。在光发射中，一个这样的量子被一个电子吸收。如果电子与阴极材料有一段距离，当它向表面移动时，会损失一些能量。当电子离开表面时，总会有一些静电成本，这就是功函数，Φ发射出的能量最高的电子将是那些非常靠近表面的电子，它们将带着动能离开阴极

在提高集电极板上的负电压，直到电流停止，即V_stop、最高动能电子（KE_e）一定有能量eV_stop离开阴极时。因此

因此，爱因斯坦的理论做出了一个非常明确的定量预测：如果入射光的频率是变化的，并且V_stop绘制为频率的函数，线的斜率应为h/e（图1.3.4A).同样明显的是，给定金属有一个最小的光频率νo，能量量子等于Φ（方程1.3.1).低于该频率的光，无论多么亮，都不会射出电子。

根据普朗克和爱因斯坦的说法，光的能量与其频率成正比，而不是与振幅成正比，会有一个最小频率ν0

需要射出没有残余能量的电子。

由于每个具有足够能量的光子只激发一个电子，因此增加光的强度（即光子数/秒）只会增加释放的电子数，而不会增加它们的动能。此外，原子不需要时间加热到临界温度，因此在吸收光时电子的释放几乎是瞬间的。最后，由于光子必须高于一定的能量才能满足功函数，因此存在一个阈值频率，低于该阈值频率则不会观察到光电子。此频率以赫兹（1/s）为单位测量，以纪念光电效应的发现者。

爱因斯坦方程1.3.1定量地解释了光电效应的性质。这个实验的一个奇怪含义是，光可以表现为一种无质量的“粒子”，现在被称为光子，其能量E=hν可以转移到实际的粒子（电子）上，从而赋予其动能，就像与台球等大质量粒子之间的弹性碰撞一样。

罗伯特·米利坎（RobertMillikan）最初不接受爱因斯坦的理论，他认为这是对光波动理论的攻击，并研究了十年，直到1916年，研究光电效应。他甚至设计了刮擦真空管内部金属表面的技术。尽管他做出了所有努力，但他发现的结果令人失望：十年后他证实了爱因斯坦的理论。在他写的论文中，米利坎仍在拼命努力避免这个结论。然而，当他发表诺贝尔奖获奖感言时，他的想法已经发生了相当大的变化！

爱因斯坦的简单解释（方程1.3.1）完全解释了Lenard和Millikan实验中观察到的现象（图1.3.4），并开始研究我们现在称为量子力学的领域。这个新领域旨在为经典力学提供量子解释，并创建更统一的物理学和热力学理论。对光电效应的研究也导致了光电子能谱新领域的创造。爱因斯坦的光电子理论提出了一种与黑体辐射完全不同的方法来测量普朗克常数。

功函数（Φ）

功函数是金属的固有特性。虽然功函数和电离能看起来是相似的概念，但它们是独立的。金属的功函数是最小能量（E）从块状（固体）金属表面去除电子（有时称为结合能）所必需的。

功函数在质量上与电离能（IE（英语）），即从气态原子或分子中去除电子所需的能量。

然而，这两种能量的星等不同（表1.3.1).例如，铜的功函数约为4.7eV，但具有更高的电离能，为7.7eV。通常，金属的电离能大于相应的功函数（即，电子在块状金属中的结合不那么紧密）。

例1.3.1：钙

a. 420nm紫光光子的能量（以焦耳和电子伏特为单位）是多少？

b. 鉴于钙金属的功函数为2.71eV，420nm紫光从钙中射出的电子的最大动能是多少？

策略

要求解（a）部分，请注意光子的能量由下式给出E=hν.对于（b）部分，一旦计算出光子的能量，就可以直接应用方程1.3.1要找到射出的电子的最大动能，由于Φ被给出。

（a）的解决方案

光子能量由下式给出

E=hν

由于我们得到的是波长而不是频率，因此我们解决了熟悉的关系c=νλ对于频率，所以

ν=c/λ

将这两个方程组合起来可以得到有用的关系

E=hc/λ

现在替换已知值会产生

转换为eV，光子的能量为

（b）的解决方案

求射出电子的动能现在是方程1.3.1.代入光子能量和结合能得到

讨论

这个420nm的紫光光子的能量只是焦耳的一小部分，因此难怪我们很难直接感知单个光子——人类更适应焦耳量级的能量。但是看一下电子伏特的能量，我们可以看到这个光子有足够的能量来影响原子和分子。例如，一个DNA分子可以用大约1eV的能量破坏，典型的原子和分子能量在eV量级，因此本例中的紫外光子可能具有生物效应。

射出的电子（称为光电子）具有相当低的能量，除非在真空中，否则它不会传播很远。电子将被0.26eV的延迟电位阻止。事实上，如果光子波长更长且其能量小于2.71eV，那么该公式将给出负动能，这是不可能的。这只是意味着具有2.96eV能量的420nm光子并没有比频率阈值高出多少。您可以自己证明阈值波长为459nm（蓝光）。这意味着，如果在测光表中使用钙金属，测光表对比蓝光更长的波长不敏感。例如，这样的测光表对红光不敏感。

总结

尽管赫兹在1887年发现了光电子，但直到1905年才提出了一种理论来完全解释这种效应。该理论是由爱因斯坦提出的，它声称电磁辐射必须被认为是一系列称为光子的粒子，它们与表面上的电子碰撞并发射它们。这一理论与电磁辐射是一种波的信念背道而驰，因此直到1916年罗伯特·米利坎（RobertMillikan）通过实验证实了该理论，它才被认为是正确的

光电效应是电磁辐射从材料中射出电子的过程。爱因斯坦提出光子是具有能量的电磁辐射的量子E=hν是辐射的频率。所有电磁辐射都由光子组成。正如爱因斯坦所解释的那样，光电效应的所有特性都是由于单个光子与单个电子的相互作用造成的。最大动能KEe射出的电子（光电子）的公式为：KEe=hν–Φ

这里hν是光子能量，Φ是电子与特定材料的功函数（或结合能）。

概念问题

1. 可见光是唯一可以引起光电效应的电磁辐射类型吗？

2. 没有光子就无法解释光电效应的哪些方面？哪些可以没有光子来解释？后者与光子的存在不一致吗？

3. 光电效应是电磁辐射的波特性还是电磁辐射的粒子特性的直接结果？简要解释一下。

4. 绝缘体（非金属）具有更高的Φ比金属，光子更难从绝缘体中射出电子。讨论这与金属中使其成为良导体的自由电荷有何关系。

5. 如果你拿起并摇晃一块金属，其中有电子可以作为电流自由移动，则不会有电子掉出来。然而，如果你加热金属，电子可能会蒸发掉。解释这两个事实，因为它们与与加热物体相比，摇动物体所涉及的能量和分布有关。

ContributorsandAttributions

l MichaelFowler(BeamsProfessor,DepartmentofPhysics,UniversityofVirginia)

l MarkTuckerman(NewYorkUniversity)

l DavidM.Hanson,EricaHarvey,RobertSweeney,TheresaJuliaZielinski("QuantumStatesofAtomsandMolecules")

l PaulFlowers(UniversityofNorthCarolina-Pembroke),KlausTheopold(UniversityofDelaware)andRichardLangley(StephenF.AustinStateUniversity)withcontributingauthors.TextbookcontentproducedbyOpenStaxCollegeislicensedunderaCreativeCommonsAttributionLicense4.0license.Downloadforfreeathttp://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).