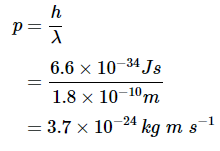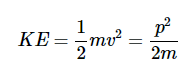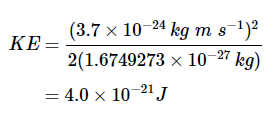1.7： 可以通过实验观察到德布罗意波

学习目标

呈现物质波粒二象性背后的实验证据

1926年G.P.Thomson和C.Davisson和L.H.Germer于1927年的电子衍射实验证实了deBroglie提议的有效性。在这些实验中，发现电子从晶体中的原子散射，并且这些散射的电子产生了干涉图样。干涉图案就像水波穿过屏障上的两个孔以产生单独的波前时产生的干涉图案，这些波前相互结合并相互干扰。这些衍射图样是波状行为的特征，由物质（例如电子和中子）和电磁辐射表现出来。如果波长与散射中心之间的间距相当，则获得衍射图样。

当波遇到大小与其波长相当的障碍物时，就会发生衍射。

继续分析导致新量子理论的实验，我们现在看看电子衍射现象。

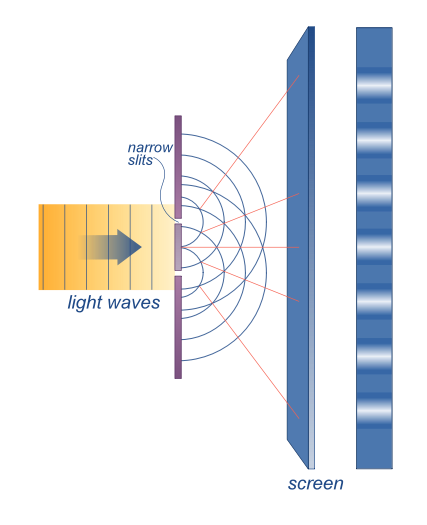
光的衍射（光作为波）

众所周知，光能够在其路径中的物体周围发生衍射，从而产生特定于物体的干涉图案。事实上，这就是全息术的工作原理（干涉图案是通过允许衍射光与原始光束干涉来创建的，这样就可以通过将原始光束照射到图像上来查看全息图）。光衍射的一个简单例子是杨氏双缝实验（图1.7.1).在这里，波形式的光（图为平行于双缝装置的平面中的波）撞击两个狭缝。然后，每个狭缝都成为球面波的点源，这些球面波随后相互干扰，从而在右侧的屏幕上产生明暗条纹。

图1.7.1：Young双缝实验。两个狭缝由平面光波照亮。

双缝实验是通过观察到的干涉直接证明波现象。这些类型的实验由ThomasYoung于1801年首次进行，以证明光的波动行为。在这个实验的基本版本中，光只照射到被两个平行狭缝刺穿的板，并且通过两个狭缝的光在板后面的屏幕上观察到（图1.7.1和1.7.2).

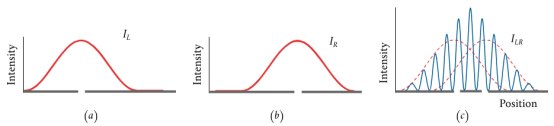
图1.7.2：通过（a）左狭缝，（b）右狭缝，（c）通过两个狭缝的颗粒振幅。在没有波长干扰行为的情况下，强度将是每个狭缝结果的总和（红色），当有干扰时，会观察到强度的明显振荡（蓝色曲线）。

光的波动性导致通过两个狭缝的光波发生干涉，在屏幕上产生明带和暗带——如果光由经典粒子组成，则不会预料到这种结果（图1.7.0c).然而，光总是被发现在屏幕的离散点被吸收，作为单个粒子（而不是波）;干涉图案是通过这些粒子在屏幕上撞击的密度变化而出现的。此外，在狭缝处包括探测器的实验版本发现，每个检测到的光子都通过一个狭缝（就像经典粒子一样），而不是通过两个狭缝（就像波一样）。

干涉是一种波现象，其中两个（或多个）波叠加形成振幅更大或更低幅度的合成波。它是用于识别波行为的主要属性。

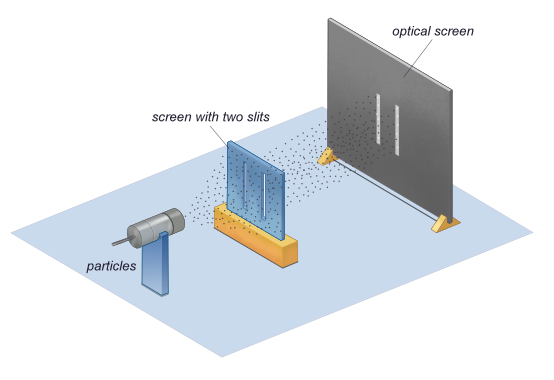
电子的衍射（电子作为波）

根据经典物理学，电子的行为应该像粒子一样——它们沿直线传播，除非受到外部因素（如磁场）的作用，否则在飞行中不会弯曲。在这个模型中，如果我们通过双缝向探测器发射一束电子束，我们应该得到两个波段的“命中”，就像你用机枪向一个有两个窗户的房子的侧面开火一样——你会得到两个区域有子弹标记的墙，其余的都完好无损（图1.7.3（上）和图1.7.2).

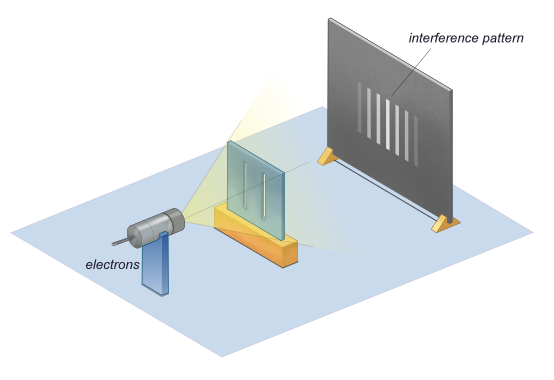
图1.7.3：（上）电子的经典模型。（下）电子的波特性。

然而，如果狭缝足够小并且足够近，我们实际上会观察到电子通过狭缝衍射并像波一样相互干扰（图1.7.3（下）和图1.7.2a，b）。这意味着电子和光子一样具有波粒二象性，这与前面讨论的德布罗意假说一致。在这种情况下，它们必须具有波长和频率等属性。我们可以从电子通过衍射光栅时的行为中推断出这些特性。

这是量子力学发展的关键结果。正如光电效应证明了光的粒子性质一样，Davisson-Germer实验也证明了物质的波动性质，并完成了波粒二象性的理论。对于物理学家来说，这个想法很重要，因为它意味着不仅任何粒子都可以表现出波特性，而且如果使用德布罗意波长，就可以使用波动方程来描述物质中的现象。

图1.7.4：基于电子波特性的扫描电子显微镜中蚂蚁的图像。

电子显微镜使用一束加速电子作为照明源。由于电子的波长可以比可见光光子的波长短100,000倍，因此电子显微镜具有比光学显微镜更高的分辨率，可以揭示较小物体的结构。透射电子显微镜可以达到优于50pm的分辨率和高达约10,000,000倍的放大倍率，而大多数光学显微镜受到衍射限制在约200nm分辨率和低于2000倍的有效放大倍率（图1.7.4).

物质是粒子还是波？

电子，实际上是任何粒子，既不是粒子也不是波。将电子描述为粒子是一种在某些情况下效果很好的数学模型，而将其描述为波是一种不同的数学模型，在其他情况下效果很好。当你选择对电子的行为进行一些计算，将其视为粒子或波时，你并不是说电子是粒子或波：你只是选择了最容易进行计算的数学模型。

中子衍射（中子作为波）

像所有量子粒子一样，中子也可以表现出波现象，如果该波长足够短，原子或其原子核可以充当衍射障碍。当从反应堆发出的中子束被减慢并通过其速度进行适当选择时，它们的波长接近1埃（0.1纳米），这是固体材料中原子之间的典型分离。然后可以使用这样的光束进行衍射实验。中子直接与原子核相互作用，对衍射强度的贡献取决于每种同位素;例如，普通氢和氘的作用不同。通常情况下，即使在存在大Z原子的情况下，轻（低Z）原子也会对衍射强度产生很大影响。

例1.7.1：中子衍射

中子没有电荷，因此它们不与原子电子相互作用。因此，它们具有很强的穿透力（例如，铅通常为10cm）。中子衍射于1934年提出，以利用德布罗意关于物质波动性质的假设。计算波长与原子间距（1.8×10⁻¹⁰m).

解答

这是deBroglie方程的简单用法

λ=hp

其中我们认识到中子的波长必须与原子间距相当（为方便起见，我们假设相等，所以λ=1.8×10⁻¹⁰m).重新排列上面的德布罗意波长关系以求解动量（p):

动能的关系为

这里v是粒子的速度。从物理常数的参考表中，中子的质量为1.6749273×10⁻²⁷kg所以

核裂变中释放的中子是“快”中子，即比这能量大得多。它们的波长远小于原子尺寸，对中子衍射没有用。我们通过引入“慢化剂”来减慢这些快中子的速度，慢化剂是中子可以穿透的材料（例如石墨），但会明显减慢。