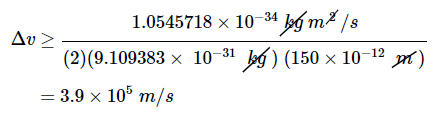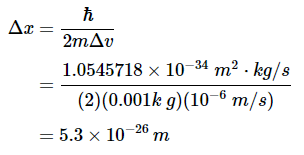1.9：海森堡不确定性原理

学习目标

要理解有时你无法了解量子系统的一切，正如海森堡不确定原理所证明的那样。

在经典物理学中，研究物理系统的行为通常是一项简单的任务，因为可以同时测量多种物理质量。然而，这种可能性在量子世界中是不存在的。1927年，德国物理学家维尔纳·海森堡（WernerHeisenberg）将这种局限性描述为海森堡不确定性原理，或简称为不确定性原理，指出不可能同时测量粒子的动量和位置。

海森堡不确定性原理是量子力学中的一个基本理论，它定义了为什么科学家不能同时测量多个量子变量。在量子力学出现之前，人们一直认为，在给定的时刻，一个物体的所有变量都可以同时精确地知道。牛顿物理学对更好的程序和技术如何减少测量不确定性没有限制，因此可以想象，只要适当小心和准确，所有信息都可以被定义。海森堡提出了一个大胆的提议，即这种精度有一个下限，这使得我们对粒子的了解本质上是不确定的。

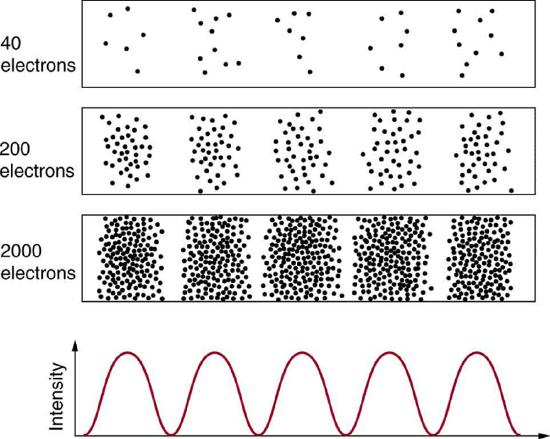
概率

物质和光子是波，意味着它们分布在一定距离内。粒子（例如电子）的位置是什么？它位于波浪的中心吗？答案在于如何测量电子的位置。实验表明，与波不同，您会在某个确定的位置找到电子。但是，如果你设置完全相同的情况并再次测量它，你会发现电子位于不同的位置，通常远离测量中的任何实验不确定性。重复测量将显示呈波浪状的位置的统计分布（图1.9.1）。

图1.9.1：从晶体表面散射的电子衍射图谱的构建。每个电子都到达一个确定的位置，无法精确预测。底部显示的总体分布可以预测为具有电子德布罗意波长的波的衍射。

在德布罗意提出物质的波动性质之后，包括薛定谔和海森堡在内的许多物理学家都探索了其后果。这个想法很快就出现了，由于其波特性，无法单独精确预测每个粒子的轨迹和目的地。然而，每个粒子都去到一个确定的地方（图1.9.1）。编译足够的数据后，您将获得与粒子波长和衍射图谱相关的分布。在给定位置找到粒子的概率是一定的，整体模式称为概率分布。那些开发量子力学的人设计了预测各种情况下概率分布的方程。

想到你无法准确预测单个粒子的去向，甚至无法跟随它到达目的地，这有点令人不安。让我们探索一下如果我们尝试跟踪一个粒子会发生什么。考虑图1.9.2中为电子和光子获得的双缝图案。当单个粒子落在探测器上时，干扰模式会随着统计而累积。这可以观察到光子或电子——现在，让我们专注于电子。你可以想象电子像任何波一样相互干扰。要测试这一点，您可以降低强度，直到狭缝和屏幕之间永远不会超过一个电子。相同的干涉图案会形成！

这意味着粒子的概率分布跨越两个狭缝，并且粒子实际上会干扰自身。这是否也意味着电子会穿过两个狭缝？电子是不可整分的物质的基本单位。但这是一个合理的问题，因此我们应该看看电子是否穿过一个狭缝或另一个狭缝，或两者兼而有之。一种可能性是在狭缝周围设置线圈，以检测穿过狭缝的电荷。观察到的是，电子总是穿过一个或另一个狭缝;它不会拆分以通过两者。

但有一个问题。如果你确定电子穿过了其中一个狭缝，你就不会再得到双狭缝图案——相反，你会得到单缝干涉。使用另一种确定电子经过哪个狭缝的方法无法逃脱。知道粒子经过一个狭缝会迫使形成单狭缝模式。如果不观察电子穿过哪个狭缝，则会获得双缝图案。知道电子穿过哪个狭缝如何改变模式？答案从根本上很重要—测量会影响被观察的系统。信息可能会丢失，在某些情况下，不可能同时以精确的精度测量两个物理量。例如，您可以通过散射光或其他电子来测量移动电子的位置。这些探针本身就有动量，通过从电子散射，它们以丢失信息的方式改变其动量。绝对知识是有限的，即使在原则上也是如此。

海森堡不确定性原理

海森堡总结说，如果人们试图测量粒子的动量和位置，那么在数学上可以表达始终存在的不确定性。首先，我们必须将变量“x”定义为粒子的位置，并将“p”定义为粒子的动量。众所周知，光子的动量就是它的频率，用比率表示h/，其中h表示普朗克常数，λ表示光子的波长。光子的位置就是它的波长(λ).为了表示数量的有限变化，希腊大写字母delta或Δ被放置在量的前面。因此

通过将Δx代入方程1.9.1中的λ，我们推导出

或

量子系统的常见趋势

公式1.9.4可以通过假设感兴趣的粒子表现得像粒子，而不是波来推导。只需让Δp=mv和Δx=h/(mv)（来自DeBroslies对粒子波长的表达式）。将mv代入第二个方程中，得到Δp，可求出方程1.9.4

.

方程1.9.4由Heisenberg和他的同事NielsBohr进一步完善，并最终改写为

其中ħ=h/2π=1.0545718×10⁻³⁴m²∙kg/s

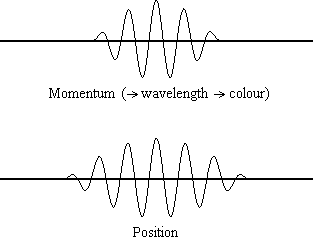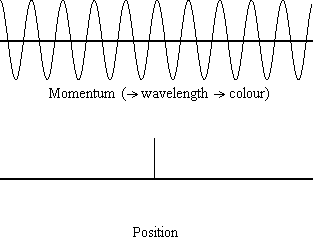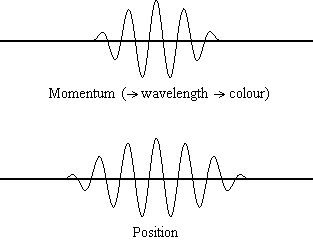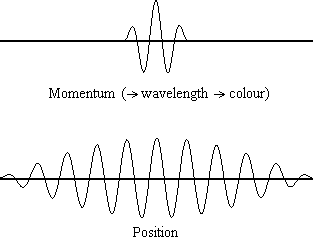
公式1.9.5表明粒子的位置越精确（Δx越小)，已知粒子在x方向上的动量(Δpx)精度越差。从数学上讲，因为必须满足不等式，所以Δx越小，Δpx将变的更大，但动量越精确，位置的精度就越低（图1.9.2 )。

图1.9.2：动画显示了光/光子（光波的相应光子粒子）的位置和动量不确定性的相关散布。从德布罗意的结果中，我们知道对于具有已知动量的粒子，p将具有一个精确的值，因为它的deBroglie波长可以确定（因此可以确定光的特定颜色）。

不确定性的正确定义是什么？

方程1.9.5关联动量和位置的不确定性。立即出现的一个问题是，如果Δx代表着全部的可能性x的值，或者如果它是一半（例如x±Δx⟩)。Δx是标准差，是x的分布的统计量值。使用一半的可能范围是更可以更加准确的估计Δx。正如我们稍后将要演示的那样，一旦我们构造了一个波函数来描述系统，那么两者x和Δx可以推导出来。然而，就目前而言方程1.9.5将起作用。

例如：如果假设一个粒子被困在一个长度为L的盒子内，那么其位置的不确定性是±L/2。那么，用于方程1.9.5的Δx应该是L/2，不是L.

例1.9.1

电子被限制在半径为150pm的镁原子的大小。其速度的最小不确定性是多少？

解答

不确定性原理（方程1.9.5):

ΔpΔx≥ħ/2

可以写成

δp≥ħ/2Δx

和代入Δp=mΔv

因为质量是确定的

Δv≥ħ/2mΔx

相关参数包括

电子质量m=me=9.109383×10⁻³¹kg

位置的不确定性：Δx=150×10⁻¹²m

通过波包和狭缝实验了解不确定性原理

大多数人很难接受不确定性原理，因为在经典物理学中，物体的速度和位置可以确定和准确地计算出来。然而，在量子力学中，电子的波粒二象性不允许我们准确计算动量和位置，因为波不在一个精确的位置，而是在太空中传播。“波包”可用于演示如何精确计算粒子的动量或位置，但不能同时计算两者。不同波长的波的累积可以组合起来，通过干涉图谱产生平均波长：这个平均波长称为“波包”。在“波包”中组合的波越多，粒子的位置就越精确，动量就越不确定，因为添加了更多不同动量的波长。相反，如果我们想要更精确的动量，我们会向“波包”添加更少的波长，然后位置会变得更加不确定。因此，没有办法同时找到粒子的位置和动量。

包括爱因斯坦在内的几位科学家都曾对不确定性原理进行过辩论。爱因斯坦创建了一个狭缝实验来试图反驳不确定性原理。他让光穿过一个狭缝，这会导致动量的不确定性，因为光在通过狭缝时表现得像一个粒子和一个波。因此，动量是未知的，但粒子的初始位置是已知的。这是一个视频，演示了通过狭缝的光粒子，随着狭缝变小，粒子的最终可能方向阵列变得更宽。当狭缝变窄时，粒子的位置变得更加精确，粒子的方向或动量变得不那么清楚，从更宽的光水平分布中可以看出。

例1.9.2

1.0g弹丸的速度已知在10⁻⁶米/秒

l 计算其位置的最小不确定性。

l 其位置的最大不确定度是多少？

解决方案a

从方程1.9.5这Δpx=mΔvx和m=1.0g.求解Δx获取

对于任何宏观对象的所有意图和目的，这都可以忽略不计。

解决方案b

对于无限（或宇宙的大小）。海森堡不确定性原则不量化是最大的不确定性。

海森堡的不确定性原理不仅帮助塑造了今天被称为量子力学的新思想流派，而且还帮助诋毁了旧理论。最重要的是，海森堡不确定性原理清楚地表明，原子的玻尔模型存在根本性错误。由于粒子的位置和动量不能同时知道，因此玻尔关于电子在围绕原子核的固定半径的圆形路径中传播的理论已经过时了。此外，海森堡的不确定性原理与量子力学中的其他革命性理论相结合，有助于塑造波动力学和当前对原子的科学理解。

幽默：海森堡与警察

海森堡因超速而被警察拦下。警官问他：“你知道你开得有多快吗？

“海森堡回答说：”不，但我们确切地知道我们在哪里！

警官困惑地看着他说：“你以每小时108英里的速度行驶！

海森堡举起双臂喊道：“太好了！现在我们迷路了！