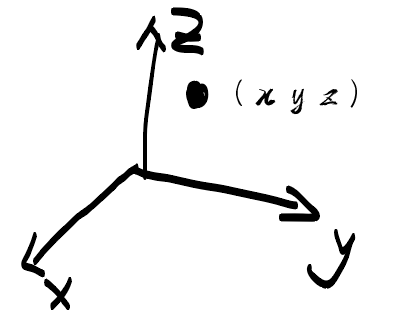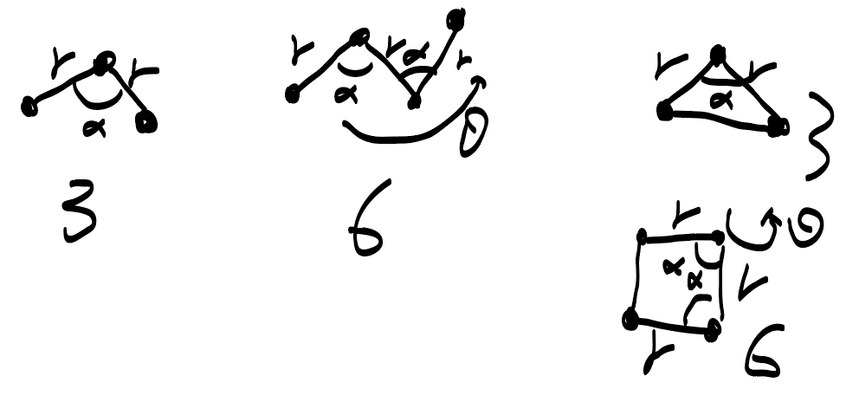能量优化基本概念-自由度

前面提及到了3N-6的维度，其实这个跟自由度有关系

大家可以再理解一下什么叫自由度

现在要确认这个球的位置（x y z）

有3个变量，说明自由度为3

自由度是指确认物体状态所需要的独立的变量个数

如上面需要 x y z

当现在N个球的时候

每个球本身3个自由度

所以3*N=3N个自由度,也就是3n个解

才能确认所有位置

但是由于合并肯定会出现减少自由度的现象

因为有关联就会减少确认位置需要的自由度

可以理解为有关联减少了不确认的未知数

在笛卡尔坐标系中，由 x, y, z三个坐标来描述

或者在球坐标系中，由 r,α，θ 三个坐标描述

刚说了一共3N个自由度，现在假设m个完整的约束，减少了计算解

那么自由度就是3n-m个

根据分子运动来说，总共三种平动，转动，振动

方法是同样的，3n-m

每个原子3种运动，共3n

平动分子不管怎么移动都是xyz，所以3种

转动如果没有对称性的，就是3个方向转动，共计3种

如果直线对称就是2个方向转动，共计2种

所以分子振动自由度一般分为3N-6,3N-5

这个与后面说的内坐标自由度不是一个概念，只是方法按照这个来

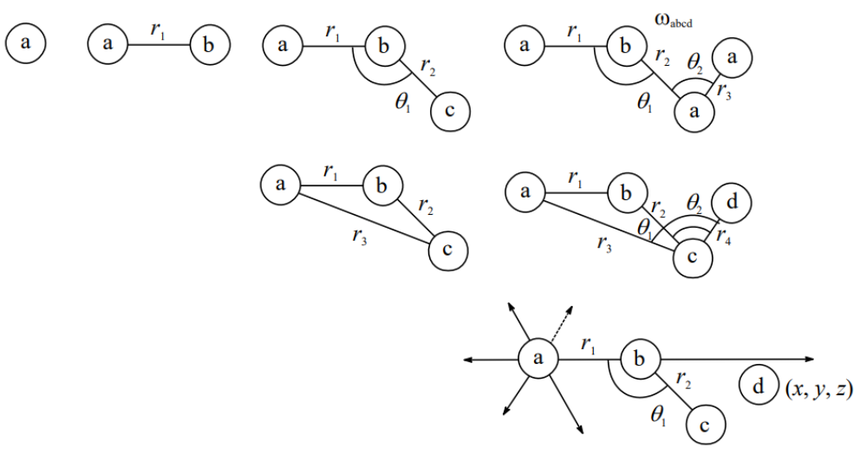
以内坐标为标准，求解其自由度3N-6（最起码3个原子），双原子为1

假设不成环，两个原子形成1个键长，N个原子n-1个键

n-2个键角，n-3个二面角

所以计算下来自由度为3N-6

如果成3环2个r，1个α就可以固定三角形，所以还是3个自由度

如果成4环，依然是3个r，2个α，1个二面角θ

把4环看成2个三角形面，所以有个二面角，其中一边的三角形固定2个r

加一个角就可以固定，这个时候可以把2个三角形共边确定，所以再加个角就可以了

关于势能面上具体学习在量化计算中好好学习

MD与QM中的能量优化是一个意思，但是目的不一样

QM必须做，MD根据实际情况也可以不做

3N-6个内坐标自由度数目