*欢迎大家去观看原文，并引用

标题：Temperature-Dependent Interfacial Performances of TiO2‑H2O withPlasmonic Metal Clusters

期刊：J. Phys. Chem. C

网址：https://doi.org/10.1021/acs.jpcc.5c02731

一、文章摘要

将二氧化钛与等离子金属相结合是一种有效提高光催化水分解制氢效率的方法。在本研究中，我们重点关注了银纳米粒子以及热等离子效应引起的温度升高对二氧化钛 -水界面性能的影响。首先，我们基于负载有银20聚集体的二氧化钛模型，结合密度泛函理论模拟，计算了在298 -368 K温度范围内二氧化钛 -水界面的性质，包括水密度、亥姆霍兹层宽度、表面静电势和水扩散系数等。结果表明，在二氧化钛表面负载银纳米粒子后，亥姆霍兹层宽度和表面静电势会减小，但水分子的吸附能会增加，水分子的层状分离现象也会减弱，这是由于银纳米粒子与二氧化钛表面的水分子之间存在相互作用所致。随着温度的升高，Ag/TiO2表面吸附的水分子数量减少，而对水分子的层状结构影响甚微。随着温度的升高，表面静电势能和扩散系数有所增强，这有利于界面反应的进行，而水分子的解吸时间则随着温度的升高迅速缩短，从而使得界面反应的理想温度约为318 K。

二、计算图文

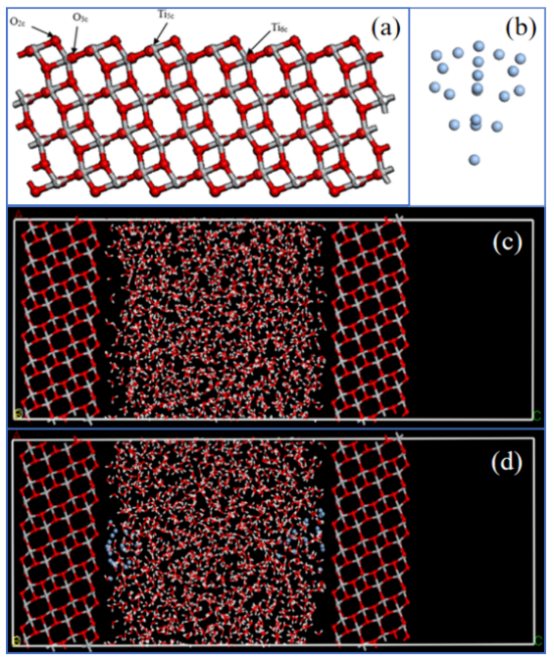
图 1.锐钛矿型 TiO2（101）的表面模型（a）、Ag20链模型的俯视图（b），以及不含（c）和含（d）Ag20链的 TiO2 - H2O系统模型，其中红色球体代表氧原子，灰色-白色球体代表钛原子，浅蓝色球体代表银原子。

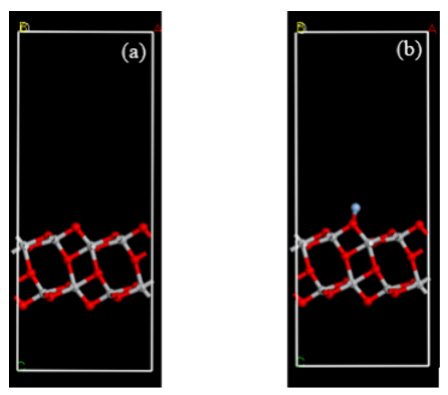
图 2.不含银原子的 TiO2表面模型（a）以及含银原子的 TiO2表面模型（b）。

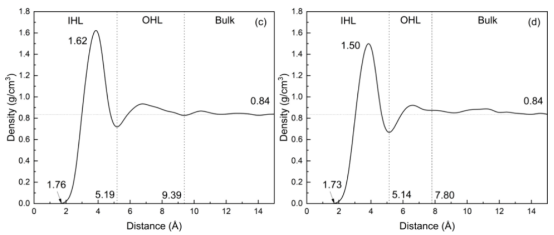
图3. 在298 K条件下，1200 皮秒时的截面图像以及 TiO2表面在无银纳米粒子（a、c）和有银纳米粒子（b、d）情况下的表面水密度分布情况。

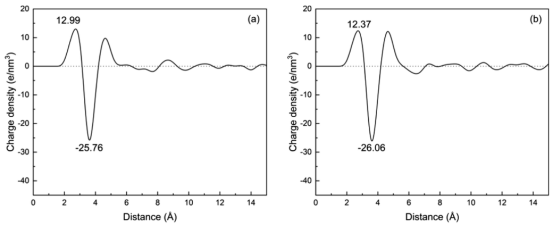
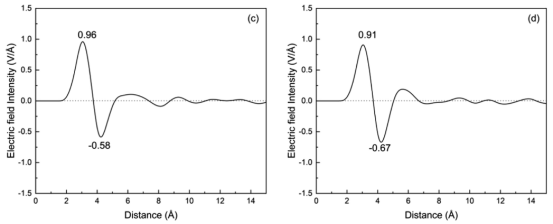
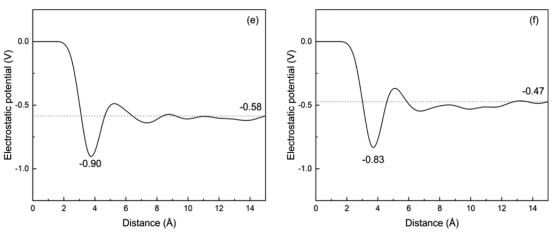
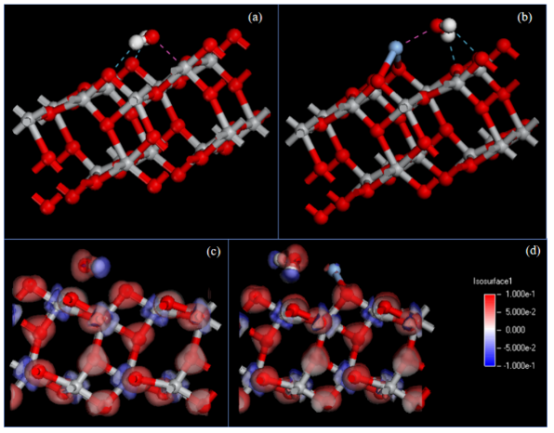
图 4.在298 K条件下，未添加银纳米粒子的 TiO2表面的电荷密度分布、电场强度分布以及界面静电势分布（a、c、e）；以及添加银纳米粒子后的 TiO2表面的上述分布（b、d、f）。

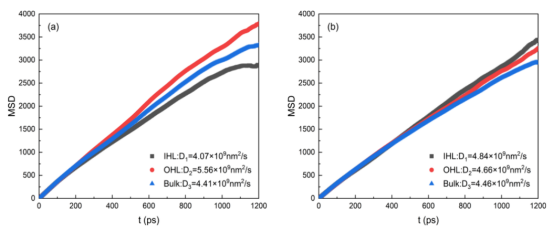
图 5.在298 K条件下，TiO2表面系统中无银纳米粒子（a）和有银纳米粒子（b）时，其内部亥姆霍兹层（IHL）、外部亥姆霍兹层（OHL）以及本体相区域（Bulk）内的水分子的 MSD曲线。

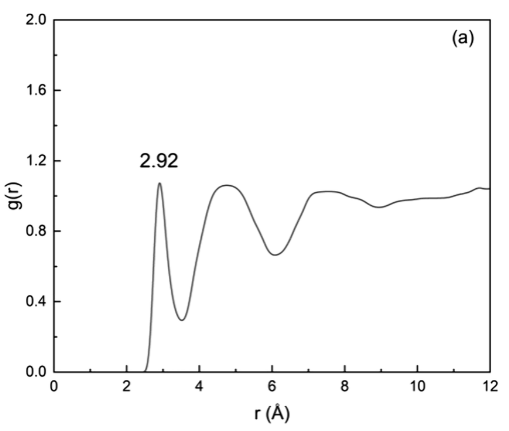
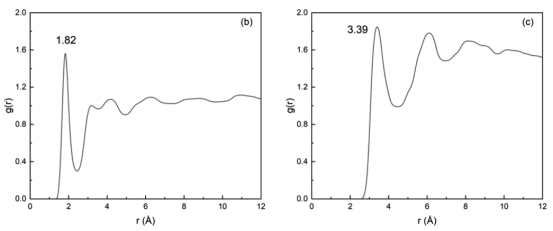
图 6.TiO2表面负载有银的体系中，Ti5c-Ow（a）、O2c-Hw（b）和 Ag-Ow（c）的径向分布函数。

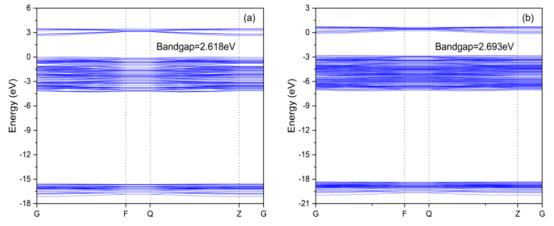
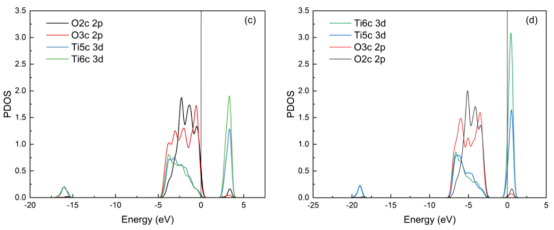
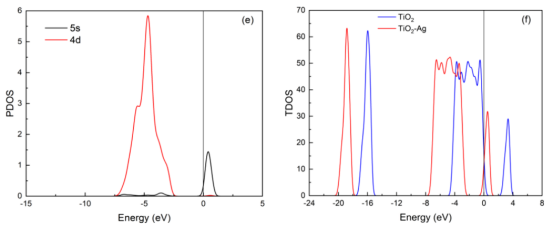
图7. TiO2 的能带结构及表面原子态密度图（a、c）和 Ag/TiO2 的能带结构及表面原子态密度图（b、d），Ag原子在 Ag/TiO2表面的态密度图（e）以及 TiO2与 Ag/TiO2 结合时的态密度图（f）。

图8.水分子在 TiO2（a、c）和 Ag/TiO2（b、d）表面的吸附结构及变形电子密度分布。蓝色虚线表示氢键，而在 a 和 b两图中红色虚线表示紧密相互作用。在 c 和 d两图中，红色和蓝色分别表示电子密度的增加和减少。

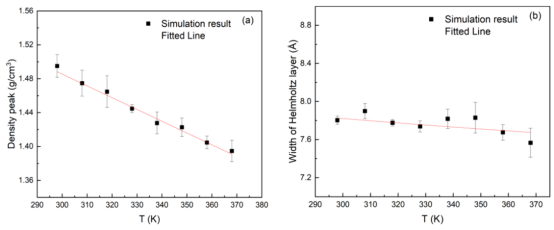
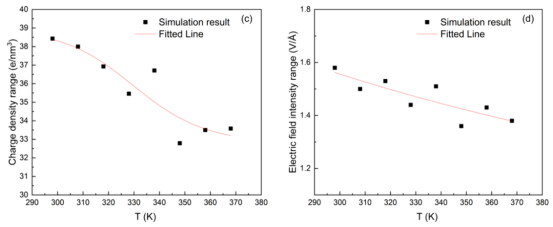
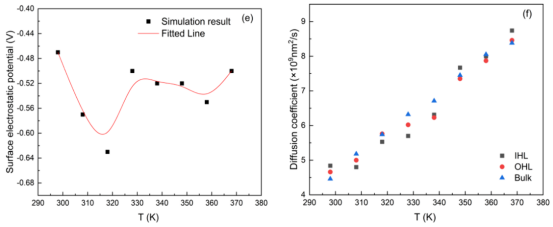
图 9 。Ag/TiO2‑H2O系统在表层水密度峰值（a）、亥姆霍兹层宽度（b）、表层电荷密度范围（c）、表层电场强度范围（d）、表层静电势（e）以及扩散系数（f）方面的温度趋势。

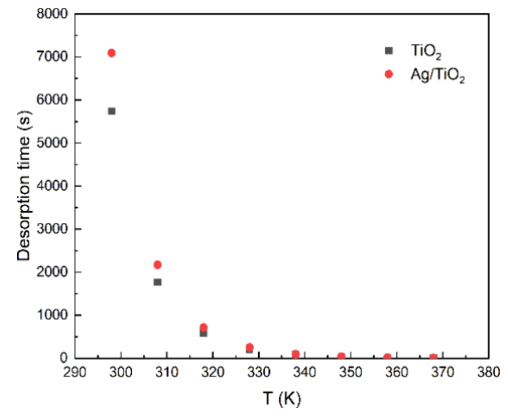
图10. 不同温度下水分子在 TiO2表面和 Ag/TiO2表面的解吸时间。

三、计算分析

3.1 界面结构与性质分析

水分子分布与双电层结构
通过分子动力学（MD）模拟TiO₂-H₂O和Ag/TiO₂-H₂O界面（298–368 K），计算：

水密度分布（图3）：量化界面附近水分子的分层结构（IHL/OHL/Bulk）。

亥姆霍兹层宽度：未负载Ag时为9.39 Å，负载后降至7.80 Å（图3c,d）。

电荷密度与电场强度：通过泊松方程（公式2-5）将电荷密度转换为界面电场强度（图4c,d）和静电势（图4e,f）。

表面静电势（驱动电荷转移的关键参数）：Ag负载使电势从0.58 V降至0.47 V。

3.2. 吸附与脱附行为

吸附位点与结合强度

径向分布函数（RDF）分析：识别Ti₅c-Ow（2.92 Å）、O₂c-Hw（1.82 Å）、Ag-Ow（3.39 Å）等吸附位点（图6）。

DFT吸附能计算：Ag/TiO₂的吸附能（0.937 eV）略高于纯TiO₂（0.932 eV）（表2）。

脱附动力学

脱附时间公式（公式8）：基于吸附能（Eₐ）和温度（T），计算水分子脱附时间（图10）。结果显示Ag延长脱附时间，但升温（>338 K）使其趋近于零。

3.3. 温度效应的定量影响

热等离子体效应的模拟

MD模拟298–368 K区间（10 K间隔）的界面性质变化：

u 水密度峰值线性下降（1.50 → 1.39 g/cm³）（图9a）。

u 界面静电势在318 K达峰值0.63 V（图9e）。

u 水扩散系数随温度升高而增加（图9f）。

最佳温度确定：结合静电势峰值与脱附时间衰减，提出318 K为反应优化温度。

四、计算方法

4.1. 分子动力学（MD）模拟

模型构建

表面模型：Anatase TiO₂(101)晶面（尺寸32.66×33.98×88.69 Å），含864个TiO₂单元和1200个水分子（表1）。

Ag纳米颗粒：Ag₂₀团簇优化后固定于表面（图1b,d）。

水模型：SPC力场（O: -0.82e, H: +0.41e），密度1 g/cm³。

参数设置

力场：COMPASS力场（公式1），涵盖键/角/二面角/静电/范德华相互作用。

系综：NVT系综，Nose-Hoover控温（弛豫时间Q=0.01）。

边界条件：周期性边界，静电作用用Ewald求和，范德华作用用Atom-based截断。

模拟时长：1200 ps，步长1.2 fs。

4.2. 密度泛函理论（DFT）计算

模型与参数

表面模型：2×2×1 TiO₂超胞（图2a），添加Ag原子模拟负载（图2b）。

泛函与基组：GGA-PBE泛函，DNP基组（含极化函数）。

收敛标准：能量（10⁻⁵ Ha）、力（0.002 Ha/Å）、位移（0.005 Å）。

k点网格：5×5×1。

分析内容

电子结构：能带（图7a,b）、态密度（PDOS/TDOS）（图7c-f）。

吸附机制：变形电子密度（图8c,d）揭示Ti₅c→Ow和Hw→O₂c的电荷转移路径。

吸附能公式：Eₐds = E_(surface+H₂O) – (E_surface + E_H₂O)。

4.3. 关键公式与算法

扩散系数计算：通过均方位移（MSD）拟合（公式6-7），斜率关联扩散系数D（图5）。

脱附时间公式：τ = ν⁻¹exp(Eₐ/k_BT)（ν=10¹² s⁻¹, k_B=8.617×10⁻⁵ eV/K）（图10）。

静电势计算：一维泊松方程积分电荷密度（公式4-5），得到界面电场和电势分布（图4）。