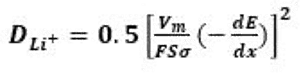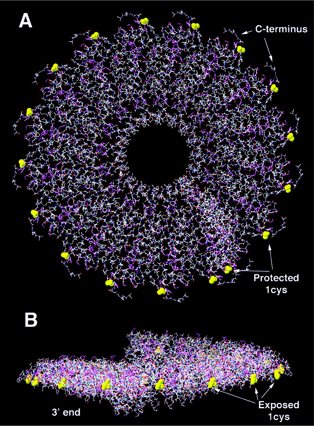
参考文献：Macromolecules 2018, 51, 8987−8995

DOI: 10.1021/acs.macromol.8b01753

PEO

PEO基结构的性质在很大程度上取决于每条链的分子量。较低分子量的结构往往更灵活，可以实现更大的Li扩散系数，尽管机械稳定性降低。为了解决这个问题，对PEO结构进行了一些修改，试图提高骨架的稳定性，包括创建嵌段共聚物，梳状和交联聚合物结构。对于足够大的分子量，扩散系数和扩散机制与链长以及聚合物端基的性质无关。聚合物电解质中锂盐的结晶可以限制聚合物电解质中载流子的有效数量，从而限制其电导率。尽管LiPF6、LiClO4和LiBF4等几种盐已经被研究过，但LiTFSI仍然是主要的候选盐，部分原因是其弥漫性电荷分布和抗团块性。

聚乙二醇（PEG），也称为聚环氧乙烷（PEO）或聚氧乙烯（POE），是指环氧乙烷的寡聚物或聚合物。这三个名称现今一般为同义词，但历史上聚乙二醇往往是指分子质量低于20,000 g/mol的低聚物和聚合物，PEO是指分子量超过20,000的聚合物，POE则可指任何分子质量的聚合物。

PEO-改性

Chem. Mater. 2007, 19, 15, 3793–3801

Langmuir 2008, 24, 3, 906–912

步骤1：PEO4-LiTFSI的离子电荷

离子扩散的模拟要求电荷小于±1的纯离子电荷，以便考虑屏蔽效应。一般来说，电荷的选择是非唯一的，需要在代表性系统上进行基于qm的仿真。

在这里，我们构建了一个PEO4-LiTFSI簇，并在B3LYP/6-31G**的理论水平上使用静电势（ESP）方法获得了+0.70的锂电荷。因此，我们选择使用±0.7的离子电荷。TFSI电荷取自分离的TFSI-分子的ESP电荷，按0.7的比例缩放，以保持中性系统。聚合物上的电荷直接取自OPLS2005力场。

这些电荷也与Mulliken电荷和后来使用PQEq方法开发的一组电荷合理一致

步骤2：PEO-LiTFSI的离子电荷

构建完成后，使用基于标度有效溶剂（SES）方法的标准程序对每个聚合物晶胞进行平衡，允许聚合物链松弛。初始平衡程序的步骤如下：

1. 以60%的实验密度构建PEO-LiTFSI结构

2. 最小化300步以避免冲突

3. 在10 K条件下运行20ps NVT给系统一个初始速度

4. 在300 K条件下运行200ps NPT以平衡晶格参数

5. 最小化300步以避免冲突

6. 在300 K条件下运行200ps NVT，使非键(静电+范德华)相互作用降低到原始值的20%(手动修改参数？还是说模拟后得到分子间作用这么低，感觉应该是前者，后者无法实现，前者可以完成这个目的)，从而使聚合物链松弛

7. 最小化300步以避免冲突

8. 在300 K条件下运行100ps NPT以重新平衡晶格参数

9. 在目标温度下运行1ns NPT以平衡晶格参数

10. 在目标温度下运行10ns的NVT以平衡聚合物。

11. 平衡过程完成后，运行115-400 ns的生产模拟。

使用软件：Desmond

力场：OPLS2005FF

对于短程相互作用，时间步长为1 fs，对于远程相互作用，时间步长为3 fs(类似gromos的双截断)

9 Å的库伦作用的cutoff

采用时间常数为τ = 1 ps的Berendsen热浴进行nvt扩散模拟

PEO−LiTFSI结构为离子浓度Li:EO(乙二醇单体) 的r = 0.02, 0.04, 0.06和0.08 。

对于r = 0.02的情况，我们还构建了链长范围为N =23、45、100和450 EO的结构。

为了在这些模拟中保持近恒定的单体数量（N = 1000），晶胞分别以m = 43、22、10和2链构建。

分别在360、400、440和480 K下进行了模拟。

一些关于PEO的实验使用甲基端链，而另一些则使用羟基端链。

动态键渗透模型

Ratner开发的动态键渗透（DynamicBondPercolation，DBP）模型提供了聚合物电解质中扩散动力学的早期描述，该模型用于描述包含一系列配位位点的无序介质中的扩散。该模型的关键假设是存在一个更新时间τR，在此时间内，由于聚合物主链的运动，相邻的配位位点会更新。该模型表明，在比更新时间（t>>τR）更长的时间尺度上，离子运动始终是扩散的。一个基于rouse的离子扩散模型由Maitra提出，后来由Borodin和Diddens进行了扩展。该模型建立在DBP更新事件描述的基础上，引入了与链内运动相关的时间尺度τ1，描述聚合物链段运动的弛豫时间τ2，以及链间跳跃之间的等待时间τ3。整体离子扩散速率可以表示为这三个事件的组合。

J. Phys. Chem. 98, 1765–1775 (1994)

J. Chem. Phys. 79, 3133–3142 (1983)

Phys. Rev. Lett. 98, 227802 (2007)

Macromolecules 43, 2028–2036 (2010)

ACS Macro Lett. 2, 322–326 (2013)

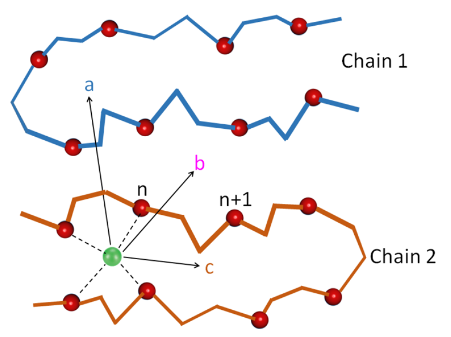
阳离子动力学可以分为三种重要的机制：（M1）沿链运动（“链内”），（M2）与链段一起运动，使用链作为载体（“节段”），（M3）在不同链之间跳跃（“链间”）

Phys. Rev. Lett. 2007, 98, 227802.

定义：锂配位模型

为了深入了解扩散的原子性质，开发了锂配位模型。每个单独的Li原子与氧配位进行分析，如果它在2.5Å以内(对方说的是引用参考文献，我更建议使用自己的rdf参数)，则认为是第一锂氧配位壳的半径。

设置n为Li与链上氧原子配位的序号平均值(假设这个Li在径向半径内的氧的序号分别是20，21，22，23，24所以平均值n为23，这个n的标注是在连续标引一条链上的氧原子)，用这个n的变化来判断Li是如何运动的，Δn则是随时间n的变化差值。Li原子配位最多的链，称为配位氧最多的链。如果出现配位氧最多的链数目相同时，Li-O距离最小的链被认为是配位最优链。我们考虑PEO-LiTFSI中Li扩散的三个事件：

(1)“链间扩散”发生在Li改变链配位并完全配位成单链时；

(2)“移位shift”是指Li从多链配位变为单链配位，但仍“粘”在链之间；

(3)“链内扩散”是指锂的最配位链保持不变，其特征是Li-O配位数目Δn的变化。

注意，典型的Li原子与4-5个氧原子配位，配位数的变化可以是分数的。分析0.25ns间隔的MD轨迹的n配位数变化。对于链内扩散（一个Li原子保持在同一链上），我们测量一个Li原子是否保持固定（Δn = 0），沿着链移动到下一个氧位点（Δn≤1），沿着链移动到两个氧位点（Δn≤2），或者移动到比两个氧位点更远的地方（Δn >2）(这个方法应该是只判断链内的，他必须根据路径进行设置序号，否则这个Δn很可能出现小于0，并且Δn的计算必须加入绝对值，否则玩意回去不就变成负数了吗)。对于链间扩散（锂原子最配位的链发生变化），可能的结果是链间跳跃，在这种情况下，锂只在末端配位到单链上，或者迁移，在这种情况下，锂至少配位到两条链上。

PEO - LiTFSI中li扩散机制的三种结果：链间扩散（情况a），平移（情况b）和链内扩散（情况c）

如果不是这样的话后续的Δn没法成立

如果是m+1与m的序号相反，那计算出来的基本Δn都要≤1

结果分析：MSD/扩散系数

聚合物中的扩散可以表现出不止一个时间尺度。在较短的时间内，粒子可能会在一个自由体积较高的局部区域停留很长时间，然后跳跃到一个新的这样的区域。为了使均方位移（MSD）与时间成正比，得到扩散常数，有必要模拟足够长的时间，使粒子能够在这些区域之间进行几次跳跃。我们发现，要达到菲克扩散的状态，在400、440和480K时需要115ns的MD时间(应该是建议增加模拟时长，但是分析的时候进行适当截取分析，而非全部进行分析)，而在360K时运行400ns的模拟。在400nsMD模拟结束时，r=0.02,N=100的聚合物结构的密度为1.125g/cm3，在实验范围内(用于判断是否合理之一)。在此离子浓度下（r=0.02），Li原子主要与PEO链上的4~6个氧原子配位(调节Li的电荷为0.7，必须满足配位数满足这个标准)。

结果分析：T与r/N的扩散系数

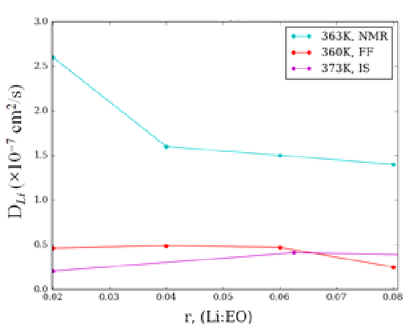
预测的360k下Li原子的扩散系数与最近的EIS实验非常吻合，从r=0.02~0.08无论是量级还是趋势都随着离子浓度的增加而减小。在文献中，这种下降的减少部分归因于盐团簇数量的增加，这在我们的模拟中没有观察到(可能是指的没有看到盐的团簇，因为前面说了非键相互作用降低，所以可能会出现这个，仅为个人猜测)。从图中了解核磁共振得到的扩散系数比EIS和我们的计算值高5倍。造成这种差异的原因需要进一步检验(建议做实验的了解)；然而，我们的扩散计算与EIS实验直接相关。在所有情况下，阴离子的扩散都比阳离子快。这一结果与报道的实验和计算数据一致，并得到了解释与TFSI阴离子与周围原子的相互作用相比，Li原子与PEO聚合物氧原子的相互作用明显更强。结果，TFSI阴离子比Li原子阳离子更自由地扩散。

结果分析：与实验对比

通过模拟（红色）、核磁共振（绿色）和EIS（紫色）测量获得的扩散系数。虽然从聚合物模拟中得到的绝对扩散系数很大程度上取决于离子电荷等参数(MD中计算精确扩散系数，这个离子电荷参数是很重要的，建议手动多次测量进行调整自己的经验数据库)，但相对扩散系数对于预测物理趋势是有用的从这些模拟中获得的Li扩散系数与EIS测量结果一致。然而，理论和EIS实验都比实验核磁共振慢约5倍。

实验内容：NMR测试扩散系数

核磁共振（NMR）波谱技术是一种非破坏性技术，它利用特定原子核的固有磁性来表征固态或液态样品中的分子结构。扩散排序波谱（DOSY）法是一种NMR实验方法，用于测定这些分子的自扩散系数D。自扩散系数是对分子迁移率的直接度量，根据能斯特-爱因斯坦关系，该系数与电导率σ存在直接关系：

在等式（1）中，F是法拉第常数，D-是阴离子的自扩散系数，D+是阳离子的自扩散常数，R是理想气体常数，T是温度。阳离子和阴离子的自扩散系数也与阳离子迁移系数t+存在直接关系。

在LiPF6等二元盐混合物的稀释极限中，阳离子迁移系数是相对于阳离子所携带的总电导率的分数。

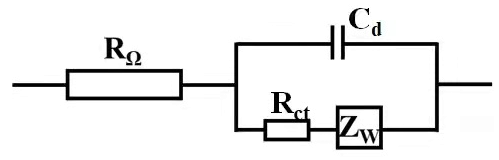
实验内容：EIS测试扩散系数

电化学阻抗谱法因其频率范围广、对系统扰动小等优势，可以有效区分电化学反应的控制步骤，是研究电极材料锂离子扩散动力学的重要工具。电极中的扩散过程会由于浓度极化而引起Warburg阻抗，电化学过程由电荷传递过程和扩散过程共同控制，则电化学系统的等效电路可简单表示为：

其中：R— 电解液和电极之间的欧姆电阻；

          C— 电极/电解液界面的双层电容；

          R— 电荷迁移电阻；

          Z— Warburg 阻抗

以平面电极的半无限扩散阻抗模型为依据结合菲克第二定律和Butler-Volmer方程，可以推导出Warburg系数σ与锂离子扩散系数之间的关系式：

其中，L — 扩散层厚度；V— 摩尔体积，cm3/mol；S — 电极表面积，cm2；dE/dx— 库伦滴定直线斜率；F — 法拉第常数；σ — Warburg常数。

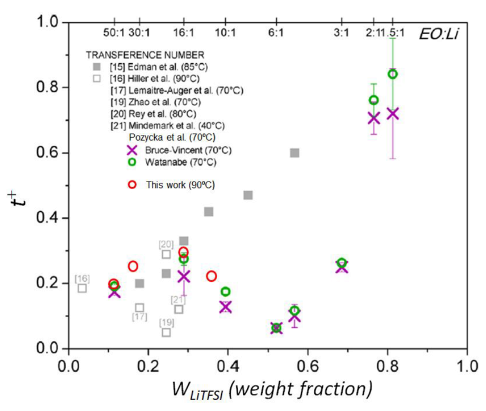
结果分析：锂迁移数目

图中PEO-LiTFSI电解质的锂迁移数值来自我们的MD模拟。我们的预测值（红色开圈）与使用Watanabe提出的公式计算的实验值（绿色开圈）非常吻合。

我们通过计算预测的离子扩散系数计算出的锂迁移数在r从0.02到0.08的变化范围内为0.2到0.3(没看到这个区域的红线圈，不懂啥意思，md往高浓走这个力场是否匹配也存在问题，所以这种计算需要注意)，这与Po˙zyczka等人在EIS实验研究中得到的值非常吻合，并再现了实验中观察到的r=0.06处的峰值。为了检验聚合物链节段运动的性质，对单个氧原子的位移进行了分析。

结果分析：主链氧位移

表计算的是温度= 360 K, r =0.02, N = 100的10链聚合物主氧的位移（Å）。分析两种极端情况下氧原子位于链（n=50,51）和位于链边缘的氧原子（n=1,100）(这里的n是指的链上的序号，所以边缘是1到100)的结果。在所有温度下，我们看到靠近聚合物链边缘的氧原子比位于链中心的氧原子位移多~30%。这表明链边缘的聚合物柔韧性增加，但这种增加的表观扩散可能并不代表真正的扩散。

结果分析：聚合物骨架的载体运动

比较表中聚合物链上的氧原子的迁移在360K下，0.25ns间隔分析下的位置变化是3.0至3.8Å。在该条件下n=0的情况下，Li位于链中的固定位置，平均位移为2.1Å。

我们看到O原子的迁移率明显高于平均Li。这似乎表明聚合物的高柔韧性可以使聚合物紧紧地抓住Li，特别是当锂被协调成多链时，减缓了锂离子的扩散。

shift是平移

Hop是链间跳跃

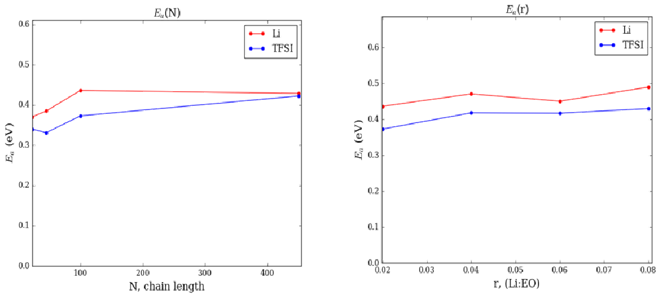
结果分析：扩散活化(激活)能图

Li和TFSI在链长N=23、45、100、450 和浓度r=0.02、0.04、0.06和0.08 Li:EO范围内的活化能(并没有说是怎么计算得到的，猜测是根据阿伦尼乌斯方程)。计算出的活化能取决于在此范围内，对链长和浓度的影响较弱，与实验测量一致。Li和TFSI离子扩散的预测活化能如所示，是链长和离子浓度的函数。这些值在Goreckiet等人报告的范围内，表明计算的扩散系数在温度范围内是可迁移的。

方法：阿伦尼乌斯方程

阿瑞尼斯方程（或公式）是化学反应的速率常数与温度之间的关系式，适用于基元反应和非基元反应，甚至某些非均相反应。其不定积分形式为：

k为反应的速率常数；

A称为指前因子/阿伦尼乌斯常数，单位与k相同；

Ea为反应的活化能，单位为焦尔每摩尔（J/mol）或千焦每摩尔（kJ/mol），在温度变化范围不大时被视为常数；

R为气体常数

T为绝对温标下的温度，单位为开尔文（K）

从阿伦尼乌斯方程可以看出，lnk随 T的变化率与活化能 Ea成正比。因此活化能越高，温度升高时反应速率增加得越快，反应速率对温度越敏感。如果同时存在多个活化能值不同的反应，则高温对活化能高的反应有利，低温对活化能低的反应有利。

对于不同温度 T下的速率常数 k值，其 lnk−1/T图应为一直线，直线的斜率和截距分别为 −Ea/R和 lnA，从此可以分别求得活化能 Ea

和指前因子 A。故活化能 Ea 也可以这样定义：

https://zh.wikipedia.org/wiki/%E9%98%BF%E4%BC%A6%E5%B0%BC%E4%B9%8C%E6%96%AF%E6%96%B9%E7%A8%8B

结果分析：扩散活化能图

Gorecki et al.用脉冲磁场梯度测量r=0.05、0.10、0.13和0.17 Li:EO得到了高分子量（N≈20,000）下锂和TFSI的实验活化能（Ea）。

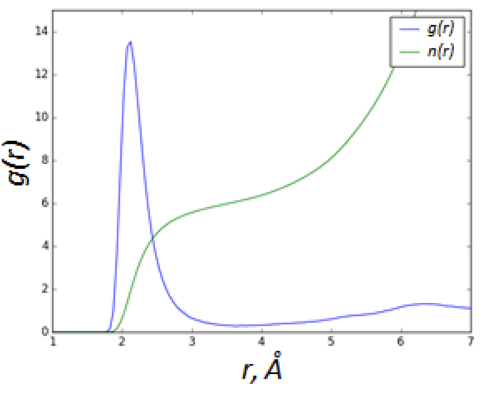
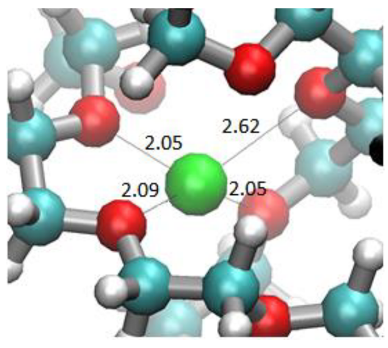
结果分析：配位数

为了理解聚合物结构中局部位点的性质，我们首先分析锂的配位。如图所示Li原子−O径向分布函数（RDF）。它对应于Li原子−OPEO键，而第二个宽峰在~6.2Å对应于Li原子−OTFSI原子对(存在问题，这个地方也有可能是OPEO，建议是直接分开进行分析，合在一起分析这种说法有问题)。积分RDF达到3Å（接近RDF中的第一个最小值）表明，平均Li原子由4.5个氧原子在2.55Å的距离内配位。

结果分析：锂配位模型

Li原子由3个聚合物O原子配位，Li原子−O原子间距离为~2.1Å，第4个O原子间距离为2.62Å。这些O原子属于两个不同的聚合物链，Li原子的位置对应于跳跃模型中的移位事件。

*从图来看啥也看不出来，2条链看不出，同时用这个距离静态数据说明移位事件并不可取，这个应该是一个动态的

结果分析：离子扩散的原子性质

为了理解PEO-LiTFSI中离子扩散的原子性质

采用配位模型对模拟时间内

(应该是扩散系数，MSD的值是对应时间的点，而不是整个轨迹)

MSD最大和最小的Li离子进行了分析

这些Li离子分别表示为最具扩散和最不具扩散的锂

MD模拟中扩散最快/慢的平均Li原子的链配位作为时间的函数

显示了该平均Li原子在MD轨迹中间隔为1ns的点上的真实位置

间隔1ns目的应该是为了更好作图

个人建议这个间隔选择与帧数一至精度更高

当然越小精度越高

点多怕不好作图，可以参考VMD使用点进行处理

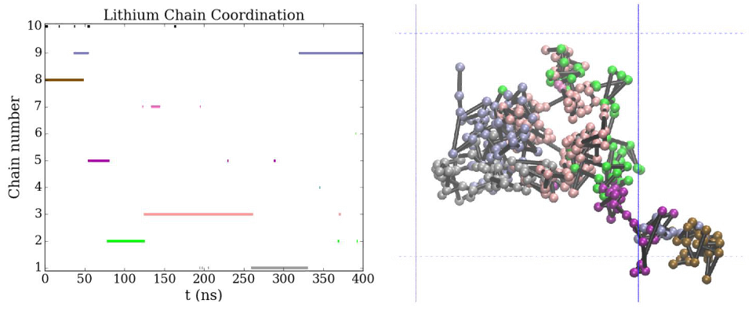
结果分析：最具扩散Li

锂原子在第8链上停留约30ns，然后跳到第9链，然后跳到第5链。在400ns的模拟时间内，最具扩散性的锂总共移动了59.3Å和坐标到7个不同的链上。这个地方的纵坐标指的是链的序号，所以分析前如果是使用gmx计算，则建议提前给PEO进行编号chain，便于后续进脚本分析，这个纵坐标出现重复的物质说明Li在两链之间活动。

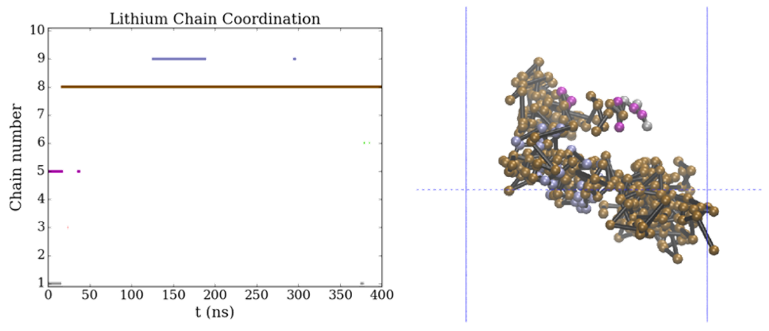
结果分析：最不具扩散Li

作为对比，本次模拟中扩散最小的这个Li原子的配位行为如图所示。在大部分模拟时间里，这个Li原子只向链8扩散了12.2Å的位移，偶尔会向链5和链9移动。因此，单个离子的扩散行为存在相当大的可变性。扩散性越强的这个Li原子在链间跳跃的频率越高，而扩散性越弱的原子只能在链间暂时移动。

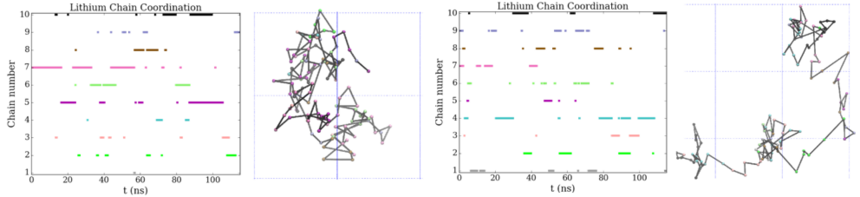
结果分析：温度对扩散的影响

这个是480K的最具/不具扩散的图，相比前面的是360K。(这个最具扩散不知道是不是反了，最好注意一下)

因为温度升高，模拟的时间也缩短了，所以分析的时间间隔也会进行缩短，使用的是0.25ns

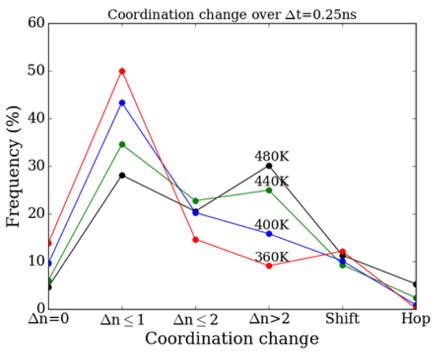
结果分析：锂配位频率

图显示了锂配位频率随温度变化的分析结果。我们发现少量这个Li原子的配位没有变化，即Δn=0。链内运动，即Δn≤1，对应于Li-O配位壳的微小变化，并且在较低温度下更频繁。温度升高与较大的内链跳数Δn的频率增加相关>2，和链间跳，这意味着一个激活屏障与这些过程有关。移位的频率，或者换句话说，尝试执行链间跳的频率，与温度相当独立，但成功尝试的次数随着温度的升高而增加，这一事实也证实了这一点。

结论

在离子浓度、温度和分子量范围内，与实验数据非常吻合。这是能够根据原子概念来解释对这些参数的扩散依赖。

我们的研究结果表明，在360K（接近电池工作温度）时，链内离子扩散是最可能的模式，但远程离子扩散在很大程度上取决于聚合物主链运动和链间跳跃扩散。

锂离子的MSD扩散速率与聚合物中心和聚合物末端的比较似乎表明，PEO聚合物过于柔韧，可能对锂离子的吸附过多(如果是说吸附过多，完全可以增加一个末端O对于Li配位数分析)。因此，锂离子倾向于在PEO的一个区域停留太长时间。这表明，柔性差的聚合物可能增加扩散系数。