*欢迎大家去观看原文，并引用

标题：Unraveling Ultrafast Li-Ion Dynamics in the Solid ElectrolyteLiTi2(PS4)3 by NMR down to Cryogenic Temperatures

期刊：J. Am. Chem. Soc.

网址：https://doi.org/10.1021/jacs.5c05253

一、文章摘要

小原子或离子的自扩散过程在众多研究领域中起着至关重要的作用。锂钛二硫化四磷（LTPS）的独特晶体结构为小锂离子载流子提供了多种能量上等效的扩散路径，并因此产生了最高的锂离子扩散系数之一。在原子尺度上单独研究这些路径具有极大的挑战性，尤其是在探究跳跃过程方面。在这项研究中，我们利用核自旋弛豫技术在低温（10 K）下进行操作，以揭示有关锂离子长程和短程动态的前所未有的详细信息。温度依赖的7Li核磁共振自旋-晶格弛豫（SLR）速率呈现出一系列扩散诱导的峰，从而能够提取活化能和跳跃速率。由于 LTPS 中锂离子局部交换过程异常迅速，要冻结锂离子动态，仅在 SLR 时间尺度上，需要低至50 K 的温度，使其完全被 LTPS 结构中的环状笼子所冻结。

二、计算图文

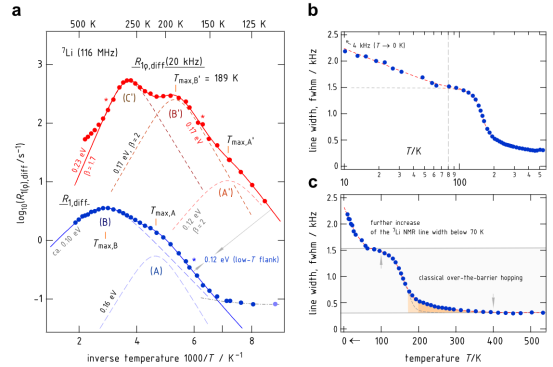
图 1.（a）记录了多晶层状硫化物（LTPS）的7Li核磁共振速率（ω0/2π =116 MHz）随温度变化的情况，并在阿伦尼乌斯表示法的框架内进行了分析，即绘制 log10(R1(ρ))与逆温度1/T 的关系图。实线表示使用两个或三个单独的速率峰值来参数化实验室（R1，ω0/2π =116 MHz）和参考旋转框架（R1ρ，ω1/2π =20 kHz）中的7Li核磁共振响应的 BPP近似值。在低温下，速率峰值进入局部区域，似乎与温度无关。从两侧（每个都用星号标记）我们可以确定 LTPS 中某些不同扩散过程的活化能。（b、c）中心过渡的7Li核磁共振线宽。（b）显示了与（c）相同的数据，但使用对数半对数图。请参阅文后解释以获取更多说明。

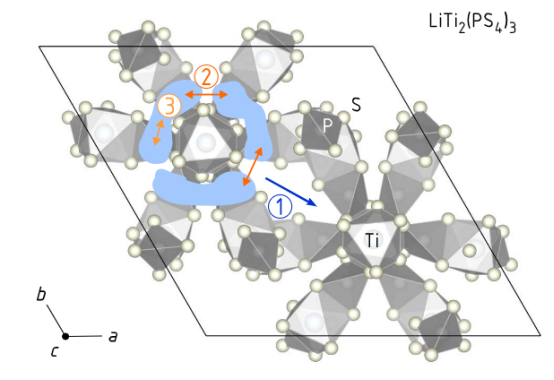
图 2.LiTi2(PS4)3 的晶体结构清晰地展现了其环状结构以及其中的锂空穴。锂离子能够在所示的三个空穴之一内移动（3），在它们之间跳跃（2），以及在环之间跳跃（1）。后一种跳跃过程是长距离传输的速率决定步骤。它很可能会涉及扩散离子所访问的间隙位置。

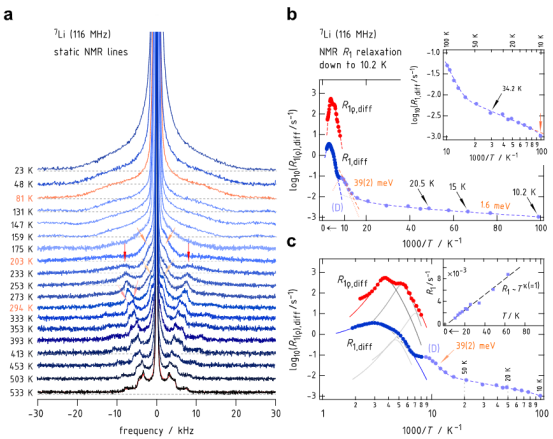
图 3.（a）在指定温度下记录的7Li（I =3/2）核磁共振谱，经过优化处理以最大程度地呈现四极矩粉末图案的变化情况。在23 K以下，宽化的四极矩图案保持不变，而中心线继续变宽，在10 K时达到2.25 kHz。在81 K处记录的谱线标志着第一个变窄步骤的结束，见图1b、c 中的动量变窄曲线。箭头表示内、外90°卫星奇点的出现。记录在533 K 的谱图后面红色实线代表一个具有 Cq =16.6 kHz 和ηq =0.19 的粉末图案模拟（见文内说明）。 （b）从10.2 K降至10 K时测量的7Li核磁共振速率的阿伦尼乌斯表示。在125 K处的局部速率峰值（标记为 D），其低温侧对应于39 meV 的活化能，转变为 R1 的线性下降，其仅表现出非常微弱的温度依赖性（1.6 meV）。图中插图以100 K至10 K 的温度标度呈现相同数据，增强了斜率变化的可见度（39 meV 对1.6 meV）。 （c）与（b）相同的阿伦尼乌斯图，但将倒数温度轴以对数标度显示。图中插图展示了在温度低于80 开尔文时 R1(T) 的线性温度依赖关系。

三、计算分析

基于文档内容，本文主要通过结合核磁共振（NMR）实验与理论模型计算，分析固态电解质LiTi₂(PS₄)₃（LTPS）中锂离子的超快动力学行为。以下是模拟计算分析的核心内容及相关计算说明：

3.1模拟计算分析的核心内容

扩散路径的激活能与跳跃速率计算

方法：利用Bloembergen-Purcell-Pound（BPP）理论模型拟合NMR弛豫速率峰。

计算对象：

通过拟合温度依赖的⁷Li NMR自旋-晶格弛豫（SLR）速率曲线（图1a），提取不同扩散路径的活化能（Eₐ）和跳跃速率（τ⁻¹）。

区分三类扩散过程：

袋内跳跃（Intrapocket, Process 3）：低活化能（0.065 eV）

袋间跳跃（Inter-pocket, Process 2）：中活化能（0.12–0.16 eV）

环间跳跃（Inter-ring, Process 1）：高活化能（0.17–0.23 eV），为长程扩散决速步。

关键参数：表1总结了BPP拟合参数（活化能、指前因子τ₀⁻¹、耦合强度C）。

量子隧穿效应的概率估算

背景：低温区（T < 60 K）弛豫速率呈现弱温度依赖性（活化能仅1.6 meV），暗示量子隧穿可能参与锂离子输运。

计算方法：

使用方形势垒模型估算⁷Li⁺隧穿概率（Tₚ）。

公式：Tₚ ≈ exp(-2d√(2mΔV/ℏ²))，其中ΔV为势垒高度，d为势垒宽度。

示例结果：

ΔV = 40 meV, d = 1 Å → Tₚ ≈ 0.002

ΔV = 20 meV, d = 0.8 Å → Tₚ ≈ 0.05

分子动力学（AIMD）模拟的验证

协作分析：结合前期发表的AIMD模拟（文献55），验证扩散路径的微观机制。

结构基础：LTPS晶体中锂离子分布于"马铃薯状"概率密度区（图2），形成环形扩散网络。

路径映射：AIMD显示锂离子在口袋内（低能垒）、口袋间（中能垒）及环间（高能垒）的跳跃过程。

活化能对比：AIMD预测长程扩散活化能（0.20 eV）与NMR结果（0.17–0.28 eV）吻合。

3.2计算与实验的协同价值

多尺度动力学关联：

AIMD模拟揭示原子尺度扩散路径 → NMR弛豫分析定量动力学参数 → PFG-NMR/阻抗谱验证长程输运。

低温机制的突破：

结合量子隧穿模型与低温NMR（低至10 K），解释传统热激活模型失效的极低温动力学行为。

结构-动力学映射：

四极耦合谱（图3a）的动态演变与AIMD预测的位点对称性变化一致，证实扩散路径的逐步激活。

3.3实验数据驱动计算模型构建

NMR弛豫速率作为计算输入

实验观测：通过变温⁷Li NMR自旋-晶格弛豫（SLR）速率测量（图1a），获得扩散诱导的速率峰（峰A、B、A'、B'、C'）。

计算关联：
采用BPP理论模型将实验曲线分解为多个扩散过程：R1(ρ)=i∑Ci1+(ωτc,i)βτc,i(i=扩散过程)

关键参数来源：

峰位置（Tmax）→ 计算跳跃速率 τ−1≈ω（如峰B'：τ−1≈1.3×105s−1）

峰宽度 → 确定不对称参数 β（表1中 β=1.7−2.0）

3.4计算模型验证实验现象

扩散路径的原子级解释

计算依据：基于前期AIMD模拟（文献55）的晶体结构（图2），预测三类扩散路径：

袋内跳跃（Process 3）

袋间跳跃（Process 2）

环间跳跃（Process 1，长程扩散决速步）

实验验证：

NMR弛豫峰活化能排序（表1）与AIMD能垒预测一致：

袋内（Ea=0.065eV）< 袋间（0.12−0.16eV）< 环间（0.17−0.23eV）

长程扩散活化能匹配：NMR峰B'（Ea=0.17eV）≈ AIMD结果（0.20eV）

四极耦合谱的动态演化

实验现象：静态⁷Li NMR谱随温度演变（图3a）：

T < 80 K：宽谱 → 扩散冻结

T = 203 K：卫星峰分裂 → 袋间/环间跳跃激活

T > 500 K：单一四极参数（Cq=16.61kHz,ηq=0.19）

计算解释：

AIMD预测的Li⁺位点对称性变化 → 直接关联EFG（电场梯度）张量重分布

跳跃速率计算值（τ−1）与谱线窄化温度点匹配（如203 K对应 τ−1∼104s−1）

3.5跨方法参数交叉验证

扩散系数量级互证

量子隧穿模型的实验支撑

计算模型：隧穿概率公式 Tp≈exp(−2d2mΔV/ℏ2)

输入参数：ΔV=20−40meV（AIMD能垒），d=0.8−1.0A˚（位点间距）

实验证据：

低温弛豫（T<60K）呈线性温度依赖 R1∝T（图3c插图）→ 电子耦合贡献

线宽持续展宽至10 K（图1b）→ 未完全冻结的量子动力学

3.6实验与计算的反馈循环

实验异常驱动模型优化：

低温区（T < 60 K）非Arrhenius行为 → 引入量子隧穿+电子耦合修正模型

计算预测引导实验设计：

AIMD指认袋内位点存在低能垒 → 针对性开展10 K超低温NMR测量（图3b）

结论：关联构建的逻辑链条

本文通过四步闭环建立计算与实验的深度关联：

实验数据作为输入：NMR弛豫谱/线形提供动力学指纹；

计算模型定量解析：BPP拟合分离多尺度扩散参数，AIMD赋予结构基础；

跨方法交叉验证：微观（DSLR）↔ 宏观（DPFG）扩散系数匹配；

模型迭代修正：实验异常（低温反常）→ 扩展量子隧穿模型。

方法论启示：这种"实验观测→模型构建→参数互证→机制迭代"框架，为复杂固态离子导体研究提供范本。

四、计算方法

4.1计算方法的详细说明

BPP理论模型的核心公式

弛豫速率表达式：

实验室坐标系：R₁ ∝ J₁(ω₀, τ_c) = C × τ_c / [1 + (ω₀τ_c)^β]

旋转坐标系：R₁ρ ∝ Jρ(ω₁, τ_c) = Cρ × τ_c / [1 + (2ω₁τ_c)^β]

参数定义：

τ_c⁻¹ = τ₀⁻¹ exp(-Eₐ/k_BT)（运动相关速率）

β：不对称参数（1 < β ≤ 2），描述弛豫峰的非对称性（β=2时为对称BPP峰）。

拟合流程：

通过最小二乘法拟合实验弛豫速率曲线（图1a）。

分离多个扩散过程对应的速率峰（例如R₁ρ中的A'、B'、C'峰）。

提取Eₐ、τ₀⁻¹、β和耦合常数C（表1）。

扩散系数（D）的微观计算

公式：D = a² / (6τ)（Einstein-Smoluchowski方程）

a：跳跃距离（环间跳跃距离≈4–4.5 Å）

τ：跳跃相关时间（由NMR速率峰顶点τ_c⁻¹ ≈ τ⁻¹确定）。

示例：189 K时，微观扩散系数D_SLR = 8.5×10⁻¹⁵ m²/s，与PFG-NMR结果（4×10⁻¹⁴ m²/s）量级一致。

量子隧穿概率的简化模型

假设：一维方形势垒，粒子质量为⁷Li⁺（m = 1.16×10⁻²⁶ kg）。

计算工具：

势垒参数（ΔV, d）基于AIMD模拟的能垒分布估算。

波函数衰减系数：κ = √(2mΔV)/ℏ。