*欢迎大家去观看原文，并引用

标题：A Perspective on Computer Simulation of Liquid Electrolytes forEnergy Storage

期刊：ACS Electrochem.

网址：https://doi.org/10.1021/acselectrochem.5c00170

一、文章摘要

在本观点中，我们探讨了用于模拟液态电解质系统的计算建模方法的现状。最近发展起来的先进模拟技术的能力为应对电解质材料设计的复杂挑战提供了重要的补充。我们讨论了常用方法（从经典的分子动力学到从头算和基于机器学习的技术）的当前优势和局限性，强调了在捕捉电解质中结构、动力学和反应性的复杂相互作用方面所固有的主要挑战。我们概述了新兴趋势，如多尺度建模和数据驱动框架，并提出了未来研究的关键方向，旨在实现预测准确性、可转移性和与实验工作的整合。

二、计算图文

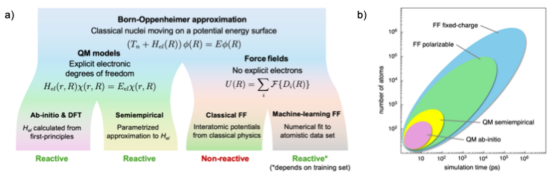
图 1.电解质原子模拟的计算方法综述。a) 量子力学方法和力场方法在电子坐标 r 的明确纳入方面有所不同。在前一种方案中，生成核力的势能是通过密度泛函理论或半经验方法获得的；而在后一种方法中，它是对适当函数的原子间距离的简单求和。b) 不同计算方法在分子动力学模拟中可实现的典型规模和时间跨度存在限制。

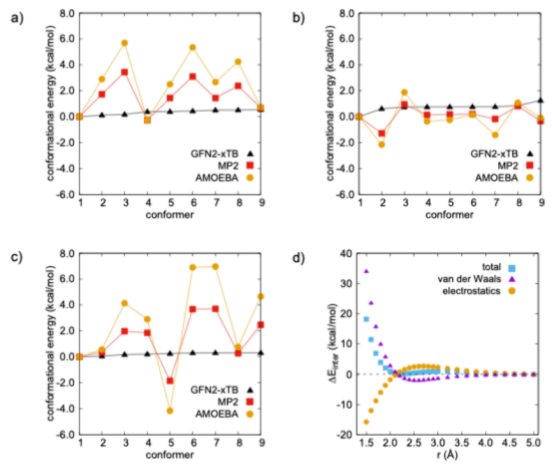
图 2.通过与气相量子力学计算（参考文献83 中的原始数据和参数）的对比，对 AMOEBA作用力场模型的性能进行了评估。图 a) - c) 分别报告了孤立的 TEG（四乙氧基乙烷）分子、(TEG)Li+复合物以及 (TEG)2二聚体的构象能量，将 AMOEBA作用力场（黄色）与 GFN2-xTB（黑色）以及 MP2/cc-pVTZ（红色）理论水平进行了比较。构象几何结构是通过 CREST89构象搜索（默认设置）获得的前九个最低能量结构。图 d)展示了 AMOEBA非键合势项（总相互作用能为蓝色、范德华力为紫色、静电势为黄色）与从 (TEG)Li+复合物沿距离增加的方向计算得出的从头算 SAPT2+3 分子间能量分解的偏差。

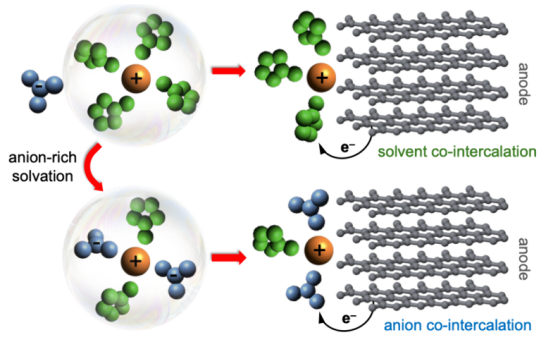
图3.高浓度电解质中富含阴离子的配位壳的示意图。绿色、蓝色和橙色的球分别代表溶剂分子、阴离子和金属阳离子。左侧的结构表示在液态中的溶剂化壳层，而右侧的结构则表示与阳极界面接触时部分解吸的阳离子结构。通过分子动力学模拟可以模拟盐浓度对金属阳离子的配位数和溶剂化结构的影响，这有助于理解电解质成分在 SEI表面化学中的作用。

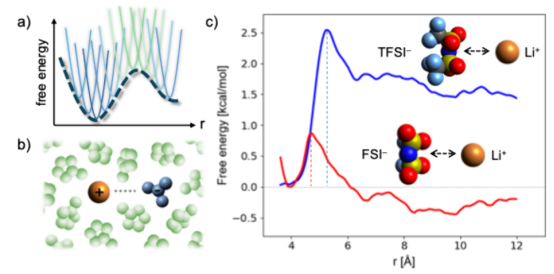
图 4.该图展示了通过伞状采样模拟实现自由能重建的过程。a) 选定的反应坐标被划分为一个小窗口，每个窗口通过应用谐波势能进行统计采样。b) 在溶液中研究离子配对的合适反应坐标是离子-离子分子间距离。c)采用加权概率分析方法（WHAM）获得的在γ-缬草内酯中锂氟离子（红色）和锂三氟离子（蓝色）离子对解离的自由能曲线。

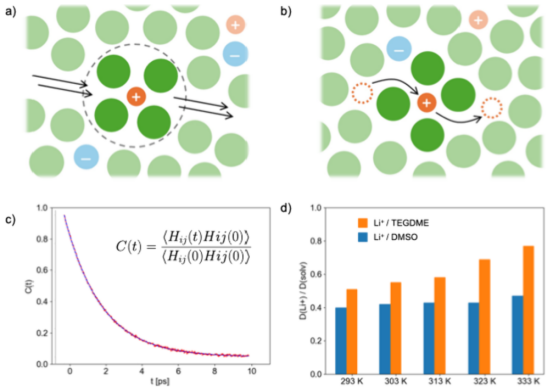
图 5.对分子动力学轨迹的动态分析可用于研究电解质中离子传输的机制。a) 在连续机制中，离子大多与完整的初级溶剂化壳层或其一部分一同移动，与扩散时间尺度相比，溶剂交换事件极为罕见。b) 在跳跃或结构扩散机制中，离子通过电解质的结构网络，通过相邻溶剂化壳层之间的连续跳跃而穿过。c)通过自相关函数 C(t)可以估算溶剂-离子或离子-离子对的平均驻留时间。括号内的内容表示集合平均值；步函数 Hij(t) 当 i 和 j之间的距离小于给定阈值时为1，否则为0；驻留时间可以通过对 C(t)进行指数拟合来推断。d)离子扩散率比 D(离子)/D(溶剂) 的温度依赖性表明在四乙二醇二甲醚（TEGDME，橙色条）和二甲基亚砜（DMSO）基电解质中发生了不同的离子传输机制（原始数据见参考文献168）。

三、计算分析

3.1结构性质：计算与光谱/散射实验互验

溶剂化结构分析

实验手段：

X射线吸收谱（EXAFS）、拉曼光谱、中子散射

计算关联：

通过AIMD或经典MD计算径向分布函数（RDF），直接对比实验的配位峰位置（如Li⁺-O距离）

模拟振动光谱：AIMD计算阴离子/溶剂振动模式，解释拉曼峰归属（如TFSI⁻的S-N-S弯曲振动）

案例：

Na⁺在DME中的配位数计算（MD）与EXAFS实验值一致（文献131）

高浓度电解质的阴离子接触离子对（CIP）结构通过计算预测，被FTIR证实（图3）

3.2动力学性质：传输参数的直接对比

扩散与电导率

实验测量：

脉冲场梯度 NMR（自扩散系数）、电化学阻抗谱（离子电导率）

计算验证：

格林-久保关系：从MD轨迹提取速度自相关函数→计算自扩散系数 D_ion

精度对比（文献159）：

黏度与传输机制

实验关联：

计算黏度（应力张量自相关积分） vs. 乌氏粘度计实测

机制解析：

通过溶剂停留时间（图5c）区分车辆/跳跃机制，解释 Dion/Dsolv 温度依赖性（实验图5d）

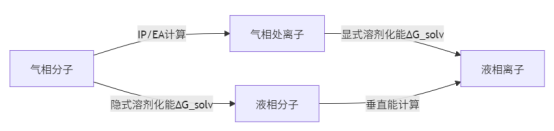
3.3电化学稳定性：计算预测实验窗口

氧化还原电位

实验基准：

线性扫描伏安法（LSV）测电化学窗口

计算方法：

热力学循环（图）：气相IP/EA + 显式溶剂化能 → 还原/氧化电位

误差控制：

隐式溶剂（SMD）平均偏差0.5 V → 显式溶剂团簇（QM/MM）降至0.2 V（文献184）

分解路径预测

实验关联：

计算TFSI⁻还原能垒 → 预测其优先于溶剂分解 → 被XPS检测到SO₂⁻产物证实（文献185）

3.4界面现象：计算指导SEI表征

SEI形成机制

实验技术：

XPS, TEM, AFM

计算关联：

AIMD模拟电极界面反应：预测EC分解生成Li₂CO₃（文献13）

自由能计算：解释添加剂（如FEC）促进LiF生成的动力学优势（文献18）

案例：高浓度电解质中阴离子分解主导SEI的计算预测 → TOF-SIMS验证（文献114）

四、计算方法

4.1. 第一性原理分子动力学（AIMD）

核心方法：

基于密度泛函理论（DFT），使用平面波基组

关键参数：

泛函选择：GGA（如PBE）或杂化泛函（如B3LYP）

截断能：>400 eV（控制基组完整性）

K点采样：仅Γ点（无序液体适用）

时间步长：0.5–1.0 fs（避免氢振动失稳）

体系限制：<500原子，<100 ps（图1b粉色区域）

半经验方法（SE）

代表模型：GFNn-xTB（紧束缚理论）

参数来源：通用原子参数化（无需体系专属拟合）

性能：比DFT快100倍（图1b黄色区域）

局限：对非标准化学环境预测偏差（如NaTFSI/EC）

4.2经典分子动力学（MD）

力场类型与参数

验证案例：
AMOEBA力场对TEG-Li⁺结合能预测误差<5%（图2d），优于GFN2-xTB

长程作用处理

静电算法：Particle Mesh Ewald（PME）

截断半径：≥1.2 nm

FFT网格密度：≥1 Å⁻³

范德华力：Lennard-Jones 12-6势

组合规则：Lorentz-Berthelot

4.3增强采样与自由能计算

伞状采样（Umbrella Sampling）

参数设置：

反应坐标：离子间距（如Li⁺-O距离）

窗口宽度：0.1–0.2 Å（覆盖0.2–1.5 nm全程）

偏置势：弹簧常数500–1000 kJ/mol·nm²

自由能重建：WHAM算法消除窗口重叠误差

传输性质计算

格林-久保公式：

自扩散系数和黏度

收敛要求：>50 ns轨迹（自相关函数衰减至0）

4.4电化学稳定性计算

热力学循环法

精度控制：

IP/EA：CCSD(T)/CBS基准（误差<0.1 eV）

溶剂化能：SMD模型（误差<0.3 eV）或显式溶剂团簇（20分子）

界面反应模拟

恒电位AIMD：施加电极表面电势（±4 V vs. Li/Li⁺）

分解路径：监测键断裂顺序（如EC的C=O优先还原）

4.5机器学习力场（ML-FF）

训练集构建：

数据来源：AIMD轨迹（>1000帧）

描述符：原子中心对称函数（ACSF）

性能对比（文献158）：

关键结论：计算精度取决于参数物理性（如AMOEBA的多极矩）和采样充分性（>50 ns）。极性力场对传输性质预测优势显著，而反应机制需量子方法支撑。